题目内容
1. 如图,Rt△ABC的∠A的平分线与过斜边中点M的垂线交于点D,求证:MA=MD.
如图,Rt△ABC的∠A的平分线与过斜边中点M的垂线交于点D,求证:MA=MD.
分析 设AD和BC交于O,由M是BC中点,可得AM=BM=CM,再根据已知条件可得∠MAD=∠CAD-∠MAC=45°-∠C=45°-(90°-∠B)=∠B-45°,因为DM⊥BC,所以∠MDA=90°-∠DOM=90°-∠BOA=∠B-45°,进而可证明∠MDA=∠MAD,所以MA=MD.
解答 证明:如图所示:设AD和BC交于O,
∵M是BC中点 ,
,
∴AM=BM=CM,
∴∠MAC=∠C,
∵AD平分∠BAC,
∴∠BAD=∠CAD=$\frac{1}{2}$∠BAC=45°,
∴∠MAD=∠CAD-∠MAC=45°-∠C=45°-(90°-∠B)=∠B-45°,
∵DM⊥BC,
∴∠MDA=90°-∠DOM,
=90°-∠BOA,
=90°-(180°-∠B-∠BAD),
=90°-(180°-∠B-45°),
=∠B-45°,
∴∠MDA=∠MAD,
∴MA=MD.
点评 本题考查了角平分线的性质、直角三角形斜边上的中线的性质以及等腰三角形的判定和性质,题目的综合性较强,难度中等,解题的关键是证明∠MDA=∠MAD,进而可得MA=MD.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
11.若关于x的不等式组$\left\{\begin{array}{l}x-m<0\\ 3-2x≤1\end{array}\right.$的所有整数解的和是10,则m的取值范围是( )
| A. | 4<m<5 | B. | 4<m≤5 | C. | 4≤m<5 | D. | 4≤m≤5 |
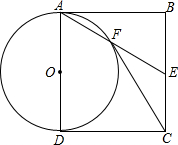 如图,四边形ABCD为矩形,E为BC边中点,连接AE,以AD为直径的⊙O交AE于点F,连接CF.
如图,四边形ABCD为矩形,E为BC边中点,连接AE,以AD为直径的⊙O交AE于点F,连接CF.
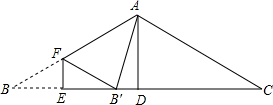 如图,△ABC中,AB=AC,∠BAC=120°,BC=6,AD⊥BC,垂足为D.E是BC上一动点,EF⊥BC,交AB于F,把∠B沿EF折叠,使点B落在点B′处.当△AB′F为直角三角形时,BE=1.
如图,△ABC中,AB=AC,∠BAC=120°,BC=6,AD⊥BC,垂足为D.E是BC上一动点,EF⊥BC,交AB于F,把∠B沿EF折叠,使点B落在点B′处.当△AB′F为直角三角形时,BE=1.