题目内容
11.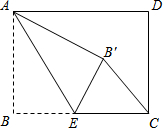 如图,在矩形ABCD中,AB=2$\sqrt{3}$,BC=4,点E是BC边上一点,连接AE,△ABE沿AE折叠,使点B落到点B′处,连接B′C,若B′C∥AE,则B′C的值为2.
如图,在矩形ABCD中,AB=2$\sqrt{3}$,BC=4,点E是BC边上一点,连接AE,△ABE沿AE折叠,使点B落到点B′处,连接B′C,若B′C∥AE,则B′C的值为2.
分析 根据平行线的性质和折叠的性质得到△B′EC是等腰三角形,于是得到CE=BE=$\frac{1}{2}$BC=2,过E作EF⊥B′C于F,根据△ABE∽△EFC,得到$\frac{BE}{CF}=\frac{AE}{CE}$,于是得到结果.
解答 解:∵B′C∥AE,
∴∠AEB=∠B′CE,∠AEB′=∠EB′C,
∵△ABE沿AE折叠得到△AB′E,
∴∠AEB=∠AEB′,BE=B′E,
∴∠EB′C=∠ECB′,
∴EB′=EC,
∴CE=BE=$\frac{1}{2}$BC=2,
过E作EF⊥B′C于F,
∴CB′=2CF,∠EFC=90°,
∵在矩形ABCD中,
∴∠B=90°,
∴∠B=∠EFC,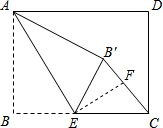
∴△ABE∽△EFC,
∴$\frac{BE}{CF}=\frac{AE}{CE}$,
∵AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=$\sqrt{(2\sqrt{3})^{2}+{2}^{2}}$=4,
∴$\frac{2}{CF}=\frac{4}{2}$,
∴CF=1,
∴B′C=2.
故答案为:2.
点评 本题考查了折叠问题:折叠前后两图形全等,即对应线段相等;对应角相等.也考查了矩形的性质以及勾股定理,证得△EB′C是等腰三角形是解题的关键.

练习册系列答案
相关题目
15.下列运算正确的是( )
| A. | 3a2•a3=3a6 | B. | 5x4-x2=4x2 | C. | (2a2)3•(-ab)=-8a7b | D. | 2x2÷2x2=0 |
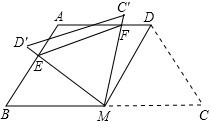 如图,等腰梯形ABCD中,AD∥BC,AD=AB=CD=2,∠C=60°,M是BC的中点.将△MDC绕点M旋转,旋转后对应的三角形为△MC′D′,当MD(即MD′)与AB交于一点E,MC(即MC′)同时与AD交于一点F时,连接EF,求证:EF∥C′D′.
如图,等腰梯形ABCD中,AD∥BC,AD=AB=CD=2,∠C=60°,M是BC的中点.将△MDC绕点M旋转,旋转后对应的三角形为△MC′D′,当MD(即MD′)与AB交于一点E,MC(即MC′)同时与AD交于一点F时,连接EF,求证:EF∥C′D′.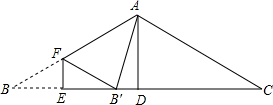 如图,△ABC中,AB=AC,∠BAC=120°,BC=6,AD⊥BC,垂足为D.E是BC上一动点,EF⊥BC,交AB于F,把∠B沿EF折叠,使点B落在点B′处.当△AB′F为直角三角形时,BE=1.
如图,△ABC中,AB=AC,∠BAC=120°,BC=6,AD⊥BC,垂足为D.E是BC上一动点,EF⊥BC,交AB于F,把∠B沿EF折叠,使点B落在点B′处.当△AB′F为直角三角形时,BE=1.