题目内容
20.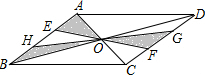 如图,?ABCD的对角线AC、BD相交于点O,EF、GH过点O,且点E、H在边AB上,点G、F在边CD上,向?ABCD内部投掷飞镖(每次均落在?ABCD内,且落在?ABCD内任何一点的机会均等)恰好落在阴影区域的概率为( )
如图,?ABCD的对角线AC、BD相交于点O,EF、GH过点O,且点E、H在边AB上,点G、F在边CD上,向?ABCD内部投掷飞镖(每次均落在?ABCD内,且落在?ABCD内任何一点的机会均等)恰好落在阴影区域的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
分析 根据平行四边形的性质易得S△OEH=S△OFG,则S阴影部分=S△AOB=$\frac{1}{4}$S平行四边形ABCD,然后根据几何概率的意义求解.
解答 解:∵四边形ABCD为平行四边形,
∴△OEH和△OFG关于点O中心对称,
∴S△OEH=S△OFG,
∴S阴影部分=S△AOB=$\frac{1}{4}$S平行四边形ABCD,
∴飞镖(每次均落在?ABCD内,且落在?ABCD内任何一点的机会均等)恰好落在阴影区域的概率=$\frac{{S}_{阴影部分}}{{S}_{平行四边形ABCD}}$=$\frac{1}{4}$.
故选C.
点评 本题考查了几何概率:求概率时,已知和未知与几何有关的就是几何概率.计算方法是长度比,面积比,体积比等.也考查了平行四边形的性质.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
11.若关于x的不等式组$\left\{\begin{array}{l}x-m<0\\ 3-2x≤1\end{array}\right.$的所有整数解的和是10,则m的取值范围是( )
| A. | 4<m<5 | B. | 4<m≤5 | C. | 4≤m<5 | D. | 4≤m≤5 |
15.下列运算正确的是( )
| A. | 3a2•a3=3a6 | B. | 5x4-x2=4x2 | C. | (2a2)3•(-ab)=-8a7b | D. | 2x2÷2x2=0 |
 关于x的不等式-2x+a≥5的解集如图所示,则a的值是3.
关于x的不等式-2x+a≥5的解集如图所示,则a的值是3. 如图,六边形ABCDEF为⊙O的内接正六边形,若⊙O的半径为2$\sqrt{3}$,则阴影部分的面积为2π-3$\sqrt{3}$.
如图,六边形ABCDEF为⊙O的内接正六边形,若⊙O的半径为2$\sqrt{3}$,则阴影部分的面积为2π-3$\sqrt{3}$.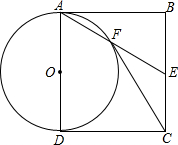 如图,四边形ABCD为矩形,E为BC边中点,连接AE,以AD为直径的⊙O交AE于点F,连接CF.
如图,四边形ABCD为矩形,E为BC边中点,连接AE,以AD为直径的⊙O交AE于点F,连接CF.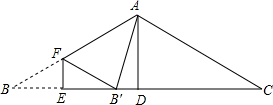 如图,△ABC中,AB=AC,∠BAC=120°,BC=6,AD⊥BC,垂足为D.E是BC上一动点,EF⊥BC,交AB于F,把∠B沿EF折叠,使点B落在点B′处.当△AB′F为直角三角形时,BE=1.
如图,△ABC中,AB=AC,∠BAC=120°,BC=6,AD⊥BC,垂足为D.E是BC上一动点,EF⊥BC,交AB于F,把∠B沿EF折叠,使点B落在点B′处.当△AB′F为直角三角形时,BE=1.