题目内容
5．已知方程组$\left\{\begin{array}{l}3x+5y=k+8\\ 3x+y=-2k\end{array}$的解满足x+y=2，则k 的值为（ ）| A． | -4 | B． | 4 | C． | -2 | D． | 2 |
分析 把k看做已知数表示出方程组的解，代入x+y=2计算即可求出k的值．
解答 解：$\left\{\begin{array}{l}{3x+5y=k+8①}\\{3x+y=-2k②}\end{array}\right.$，
①-②得：4y=3k+8，
解得：y=$\frac{3k+8}{4}$，
②×5-①得：12x=-11k-8，
解得：x=-$\frac{11k+8}{12}$，
代入x+y=2中得：$\frac{3k+8}{4}$-$\frac{11k+8}{12}$=2，
去分母得：9k+24-11k-8=24，
解得：k=4，
故选B
点评 此题考查了二元一次方程组的解，方程组的解即为能使方程组中两方程都成立的未知数的值．
练习册系列答案
中考解读考点精练系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
相关题目
13．
如图，矩形ABCD，以A为圆心，AD为半径作弧交BC于点F，交AB的延长线于点E，已知 AD=4，AB=2$\sqrt{2}$，则阴影部分的面积为（ ）
如图，矩形ABCD，以A为圆心，AD为半径作弧交BC于点F，交AB的延长线于点E，已知 AD=4，AB=2$\sqrt{2}$，则阴影部分的面积为（ ）| A． | 2π-4 | B． | $\frac{π}{2}+4$ | C． | $\frac{π}{2}$-8 | D． | $\frac{π}{2}+8$ |
20．把所有正奇数从小到大排列，并按如下规律分组：（1）（3，5，7）、（9，11，13，15，17），（19，21，23，25，27，29，31），…，现有等式Am=（i，j）表示正奇数m是第i组第j个数（从左往右数），如A7=（2，3），则A89=（ ）
| A． | （6，7） | B． | （7，8） | C． | （7，9） | D． | （6，9） |
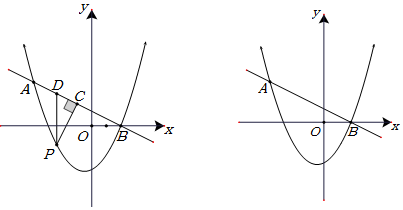
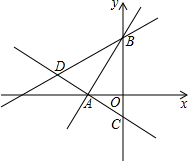如图，在平面直角坐标系中，已知点A（-$\sqrt{3}$，0），B（0，3），C（0，-1）三点．
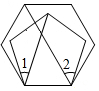正五边形和正六边形按如图所示的位置进行摆放，则∠2-∠1的度数为34°．
15．若（9m+1）2=316，则正整数m的值为（ ）
| A． | 2 | B． | 3 | C． | 4 | D． | 5 |