题目内容
13. 如图,矩形ABCD,以A为圆心,AD为半径作弧交BC于点F,交AB的延长线于点E,已知 AD=4,AB=2$\sqrt{2}$,则阴影部分的面积为( )
如图,矩形ABCD,以A为圆心,AD为半径作弧交BC于点F,交AB的延长线于点E,已知 AD=4,AB=2$\sqrt{2}$,则阴影部分的面积为( )| A. | 2π-4 | B. | $\frac{π}{2}+4$ | C. | $\frac{π}{2}$-8 | D. | $\frac{π}{2}+8$ |
分析 连接AF,根据勾股定理求出BF,求出∠BAF的度数,根据扇形面积公式、三角形的面积公式计算即可.
解答 解: 连接AF,
连接AF,
由题意得,AF=AD=4,
由勾股定理得,BF=$\sqrt{A{F}^{2}-A{B}^{2}}$=2$\sqrt{2}$,
∴∠BAF=45°,
∴阴影部分的面积=$\frac{45×π×{4}^{2}}{360}$-$\frac{1}{2}$×2$\sqrt{2}$×2$\sqrt{2}$=2π-4,
故选:A.
点评 本题考查的是矩形的性质、扇形面积计算,掌握扇形面积公式、矩形的性质是解题的关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
3.下列计算正确的是( )
| A. | 2a+3b=5ab | B. | a6÷a3=a2 | C. | (a+b)2=a2+b2 | D. | $\sqrt{12}$-$\sqrt{3}$=$\sqrt{3}$ |
4.若点P(2k-1,2-k)在第二象限,则k的取值范围是( )
| A. | k<$\frac{1}{2}$ | B. | k<2 | C. | $\frac{1}{2}$<k<2 | D. | k>2 |
18.当x=3时,下列不等式成立的是( )
| A. | x+3>5 | B. | x+3>6 | C. | x+3>7 | D. | x+3<5 |
2.今年参观“5•18”海交会的总人数约为489500人,将数据489500用科学记数法表示为( )
| A. | 48.95×104 | B. | 4.895×104 | C. | 4.895×105 | D. | 0.4895×106 |
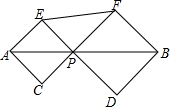 如图,AB=4,P在线段AB上,以.AP,BP为对角线,作正方形AEPC与正方形BFPD,则EF的最小值为2.
如图,AB=4,P在线段AB上,以.AP,BP为对角线,作正方形AEPC与正方形BFPD,则EF的最小值为2.


