题目内容

14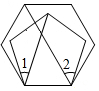．正五边形和正六边形按如图所示的位置进行摆放，则∠2-∠1的度数为34°．

分析 根据正多边形的内角，可得∠1，2，根据角的和差，可得答案．

解答 解：正五边形的内角是$\frac{（5-2）×180}{5}$=108°，
∠1=$\frac{180°-108°}{2}$=26°，
正六边形的内角为$\frac{（6-2）×180°}{6}$=120°，
∠2=180°120°=60°，
∠2-∠1=60°-26°=34°，
故答案为：34°．

点评 本题考查了多边形的内角与外角，利用证多边形的内角得出正五边形的内角、正六边形的内角是解题关键．

练习册系列答案
相关题目
4．若点P（2k-1，2-k）在第二象限，则k的取值范围是（　　）
A．k＜$\frac{1}{2}$B．k＜2C．$\frac{1}{2}$＜k＜2D．k＞2
5．已知方程组$\left\{\begin{array}{l}3x+5y=k+8\\ 3x+y=-2k\end{array}$的解满足x+y=2，则k 的值为（　　）
A．-4B．4C．-2D．2
2．今年参观“5•18”海交会的总人数约为489500人，将数据489500用科学记数法表示为（　　）
A．48.95×104B．4.895×104C．4.895×105D．0.4895×106
9．如果把一个奇数位的自然数各数为上的数字从最高位到个位依次排列，与从个位到最高位依次排列出的一串数字完全相同，相邻两个数位上的数字之差的绝对值相等（不等于0），且该数正中间的数字与其余数字均不同，我们把这样的自然数称为“阶梯数”，例如自然数12321，从最高位到个位依次排出的一串数字是：1，2，3，2，1，从个位到最高位依次排出的一串数字仍是：1，2，3，2，1，且|1-2|=|2-3|=|3-2|=|2-1|=1，因此12321是一个“阶梯数”，又如262，85258，…，都是“阶梯数”，若一个“阶梯数”t从左数到右，奇数位上的数字之和为M，偶数位上的数字之和为N，记P（t）=2N-M，Q（t）=M+N．
（1）已知一个三位“阶梯数”t，其中P（t）=12，且Q（t）为一个完全平方数，求这个三位数；
（2）已知一个五位“阶梯数”t能被4整除，且Q（t）除以4余2，求该五位“阶梯数”t的最大值与最小值．
19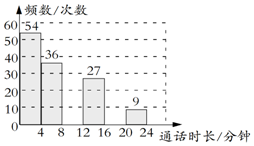．手机在现如今的社会几乎是每人一部，在近期的一项研究结果显示，普通用户平均每天查看手机大约110次，其中大约22次是打电话．小乔想了解家人打电话的通话时长（即每次的通话时间）的分布情况，于是他收集了他家800个通话时长的数据，这些数据均不超过24分钟，他从中随机选取了若干个数据作为样本，统计结果如下表，并将结果绘制成如图所示的频数分布直方图．
通话时长x/分钟次数
0＜x≤454
4＜x≤836
8＜x≤124a
12＜x≤1627
16＜x≤204a
20＜x≤243a
（1）a的值为3；补全频数分布直方图；
（2）样本中通话时长在20＜x≤24之间的9个数据分别为21分08秒，22分25秒，22分14秒，21分23秒，23分48秒，21分02秒，23分16秒，23分42秒，21分17秒，求这9个通话时长的平均数；
（3）请估计小乔家这800个通话中通话时长超过12分钟的次数．
6．若方程组$\left\{\begin{array}{l}{2x+y=5}\\{x+2y=a-3}\end{array}\right.$的解满足x+y的值为非负数，则a满足（　　）
A．a＜-2B．a≤-2C．a≤2D．a≥-2
3．一次函数y=kx+b，当k＜0，b＜0时，它的图象大致为（　　）
A．B．C．D．
4．已知，如图AB=CD，E、F在AC上，∠AFB=∠CED=90°，AE=CF，求证：AB∥DC．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网