题目内容
10.如图,在平面直角坐标系中,直线y=-$\frac{1}{2}$x+1与抛物线y=ax2+bx-3交于A、B两点,点B在x轴上,点A的纵坐标为3.点P是直线AB下方的抛物线上一动点(不与A、B点重合),过点P作x轴的垂线交直线AB于点D,作PC⊥AB于点C.
(1)求a、b及sin∠BDP的值;
(2)设点P的横坐标为m;
①用含有m的代数式表示线段PD的长,并求出线段PC的最大值;
②连接PA,线段PD把△PAC分成两个三角形,是否存在适合的m值,使这两个三角形的面积之比为8:9?若存在,请求出m的值;若不存在,说明理由.
③是否存在点P使得由点P、C、A组成的三角形与△PCD相似?若存在,请求出点P的坐标;若不存在,请说明理由.
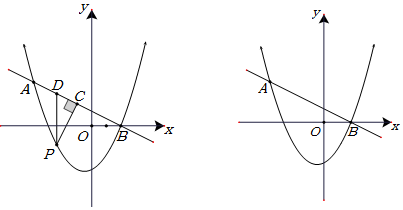
分析 (1)先求出A、B点的坐标,将其代入抛物线解析式即可,而求sin∠BPD的值时,转化为求sin∠BAF即可;
(2)①求出P、D坐标,在Rt△PDC中,利用(1)中结论,解直角三角形即可,最后利用二次函数的性质即可解决问题;
②如图2中,假设存在这样的点P,延长PD,过点A作AM⊥PD于M点,过点C作CN⊥PD于N点.分两种情形,构建方程即可解决问题;
③存在.如图3中,连接PA交x轴于Q.作AH⊥x轴于H.首先证明AQ=QB,在Rt△AHQ中,构建方程求出点Q的坐标,求出直线AQ,利用方程组即可解决问题;
解答 解:(1)过点A做AF⊥x轴于点F,如图1,
∵点B在x轴上,点A的纵坐标为3,且A、B两点均在直线y=-$\frac{1}{2}$x+1上,
∴将y=0与y=3代入直线方程解得x=2,x=-4,
∴点B(2,0),点A(-4,3),
∴BF=2-(-4)=6,AF=3-0=3,AB=$\sqrt{A{F}^{2}+B{F}^{2}}$=3 $\sqrt{5}$,
∵A、B两点在抛物线上,
∴$\left\{\begin{array}{l}{4a+2b-3=0}\\{16a-4b-3=3}\end{array}\right.$,解得 $\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=\frac{1}{2}}\end{array}\right.$,
∴抛物线解析式为y=$\frac{1}{2}$x2+$\frac{1}{2}$x-3.
∵PD⊥x轴,AF⊥x轴,
∴∠BDP=∠BAF,
∴sin∠BDP=sin∠BAF=$\frac{BF}{AB}$=$\frac{6}{3\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$.
(2)①如图1中,∵P点坐标为(m,$\frac{1}{2}$m2+$\frac{1}{2}$m-3),D点坐标为(m,1-$\frac{1}{2}$m),
PD=1-$\frac{1}{2}$m-( $\frac{1}{2}$m2+$\frac{1}{2}$m-3)=-$\frac{1}{2}$m2-m+4,
PC=PD•cos∠CPD=-$\frac{\sqrt{5}}{5}$m2-$\frac{2\sqrt{5}}{5}$m+$\frac{8\sqrt{5}}{5}$=-$\frac{\sqrt{5}}{5}$(m+1)2+$\frac{9\sqrt{5}}{5}$,
当m=-1时,PC最大,此时PC=$\frac{9\sqrt{5}}{5}$.
②如图2中,假设存在这样的点P,延长PD,过点A作AM⊥PD于M点,过点C作CN⊥PD于N点.
∵P点坐标为(m,$\frac{1}{2}$m2+$\frac{1}{2}$m-3),D点坐标为(m,1-$\frac{1}{2}$m),A点坐标(-4,3),
∴AM=4+m,
∵CN=PC•sin∠DPC=$\frac{\sqrt{5}}{5}$PC=-$\frac{1}{5}$m2-$\frac{2}{5}$m+$\frac{8}{5}$,
∵AM∥CN,
∴$\frac{AD}{CD}$=$\frac{AM}{CN}$,
∵线段PD把△PAC分成两个三角形,使这两个三角形的面积比为8:9,
∴当$\frac{AD}{CD}$=$\frac{AM}{CN}$=$\frac{8}{9}$,即$\frac{4+m}{-\frac{1}{5}{m}^{2}-\frac{2}{5}m+\frac{8}{5}}$=$\frac{8}{9}$,
整理得8m2+61m+116=0,解得m=-$\frac{29}{8}$或-4(舍弃),
当$\frac{AD}{CD}$=$\frac{AM}{CN}$=$\frac{9}{8}$,即$\frac{4+m}{-\frac{1}{5}{m}^{2}-\frac{2}{5}m+\frac{8}{5}}$=$\frac{9}{8}$,
整理得9m2+58m+88=0,解得m=-$\frac{22}{9}$或-4(舍弃)
综上所述,m的值为-$\frac{29}{8}$或-$\frac{22}{9}$.
③存在.
理由:如图3中,连接PA交x轴于Q.作AH⊥x轴于H.
∵△CPD∽△CAP,
∴∠CPA=∠CAQ,
∵∠CPD=∠ABQ,
∴∠QAB=∠QBA,
∴QA=QB,设QA=QB=x,
在Rt△AHQ中,x2=32+(6-x)2,解得x=$\frac{15}{4}$,
∴OQ=$\frac{7}{4}$,
∴Q(-$\frac{7}{4}$,0),
∴直线AQ的解析式为y=-$\frac{4}{3}$x-$\frac{7}{3}$,
由$\left\{\begin{array}{l}{y=-\frac{4}{3}x-\frac{7}{3}}\\{y=\frac{1}{2}{x}^{2}+\frac{1}{2}x-3}\end{array}\right.$解得$\left\{\begin{array}{l}{x=-4}\\{y=3}\end{array}\right.$或$\left\{\begin{array}{l}{x=\frac{1}{3}}\\{y=-\frac{25}{9}}\end{array}\right.$,
∴点P的坐标为($\frac{1}{3}$,-$\frac{25}{9}$).
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征和二次函数的性质;会利用待定系数法求函数的解析式,会通过解方程或方程组求函数与坐标轴的交点坐标和两个函数图象的交点坐标;会运用勾股定理、锐角三角函数和相似比进行几何计算;理解坐标与图形性质.

| A. | x+3>5 | B. | x+3>6 | C. | x+3>7 | D. | x+3<5 |
| A. | 48.95×104 | B. | 4.895×104 | C. | 4.895×105 | D. | 0.4895×106 |
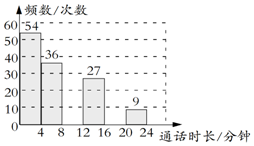 手机在现如今的社会几乎是每人一部,在近期的一项研究结果显示,普通用户平均每天查看手机大约110次,其中大约22次是打电话.小乔想了解家人打电话的通话时长(即每次的通话时间)的分布情况,于是他收集了他家800个通话时长的数据,这些数据均不超过24分钟,他从中随机选取了若干个数据作为样本,统计结果如下表,并将结果绘制成如图所示的频数分布直方图.
手机在现如今的社会几乎是每人一部,在近期的一项研究结果显示,普通用户平均每天查看手机大约110次,其中大约22次是打电话.小乔想了解家人打电话的通话时长(即每次的通话时间)的分布情况,于是他收集了他家800个通话时长的数据,这些数据均不超过24分钟,他从中随机选取了若干个数据作为样本,统计结果如下表,并将结果绘制成如图所示的频数分布直方图.| 通话时长x/分钟 | 次数 |
| 0<x≤4 | 54 |
| 4<x≤8 | 36 |
| 8<x≤12 | 4a |
| 12<x≤16 | 27 |
| 16<x≤20 | 4a |
| 20<x≤24 | 3a |
(2)样本中通话时长在20<x≤24之间的9个数据分别为21分08秒,22分25秒,22分14秒,21分23秒,23分48秒,21分02秒,23分16秒,23分42秒,21分17秒,求这9个通话时长的平均数;
(3)请估计小乔家这800个通话中通话时长超过12分钟的次数.
| A. | 小郭荡秋千运动 | B. | 月亮绕地球运动 | ||
| C. | 东风-5A洲际导弹击中目标后爆炸 | D. | 算盘上拨珠子 |
