题目内容
8. 如图,已知抛物线m经过原点O,与x轴交于点A(-3,0),P为抛物线的顶点将抛物线m平移后得到抛物线y=(x+$\frac{3}{2}$)2,其中点A,P,O的对应点分别为A′,P′,O′,连接AA′,则图中阴影部分的面积为$\frac{27}{4}$.
如图,已知抛物线m经过原点O,与x轴交于点A(-3,0),P为抛物线的顶点将抛物线m平移后得到抛物线y=(x+$\frac{3}{2}$)2,其中点A,P,O的对应点分别为A′,P′,O′,连接AA′,则图中阴影部分的面积为$\frac{27}{4}$.
分析 利用抛物线的平移可得到抛物线m的解析式为y=(x+$\frac{3}{2}$)2-$\frac{9}{4}$,从而可判断抛物线m向上平移$\frac{9}{4}$个单位得到抛物线y=(x+$\frac{3}{2}$)2,由于图中阴影部分的面积等于平行四边形OAA′O′的面积,然后根据平行四边形的面积公式求解.
解答 解:抛物线m的解析式为y=x(x+3),则y=x2+3x=(x+$\frac{3}{2}$)2-$\frac{9}{4}$,
所以抛物线m向上平移$\frac{9}{4}$个单位得到抛物线y=(x+$\frac{3}{2}$)2,
而图中阴影部分的面积等于线段OA向上平移$\frac{9}{4}$个单位所扫过的面积,
即图中阴影部分的面积等于平行四边形OAA′O′的面积,
所以图中阴影部分的面积=3×$\frac{9}{4}$=$\frac{27}{4}$.
故答案为$\frac{27}{4}$.
点评 由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式

练习册系列答案
相关题目
18.已知,圆锥的高h=$2\sqrt{3}$cm,底面半径r=2cm,则圆锥的侧面积为( )cm2.
| A. | 4$\sqrt{3}$π | B. | 8π | C. | 12π | D. | (4$\sqrt{3}$+4)π |
19.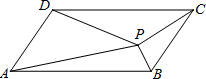 如图,平行四边形ABCD中,P是形内任意一点,△ABP,△BCP,△CDP,△ADP的面积分别为S1,S2,S3,S4,则一定成立的是( )
如图,平行四边形ABCD中,P是形内任意一点,△ABP,△BCP,△CDP,△ADP的面积分别为S1,S2,S3,S4,则一定成立的是( )
 如图,平行四边形ABCD中,P是形内任意一点,△ABP,△BCP,△CDP,△ADP的面积分别为S1,S2,S3,S4,则一定成立的是( )
如图,平行四边形ABCD中,P是形内任意一点,△ABP,△BCP,△CDP,△ADP的面积分别为S1,S2,S3,S4,则一定成立的是( )| A. | S1+S2=S3+S4 | B. | S1+S2>S3+S4 | C. | S1+S3=S2+S4 | D. | S1+S2<S3+S4 |
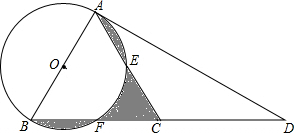 如图,在△ABC中,AC=BC,延长BC到点D,使CD=CB,连接AD,以AB为直径作⊙O,分别交AC、BC于点E、F
如图,在△ABC中,AC=BC,延长BC到点D,使CD=CB,连接AD,以AB为直径作⊙O,分别交AC、BC于点E、F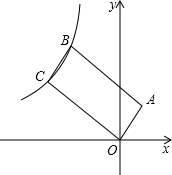 如图,反比例函数y=$\frac{k}{x}$(x<0)的图象经过平行四边形OABC的两个顶点B,C,若点A的坐标为(1,2),AB=$\sqrt{5}$BC,则反比例函数的解析式为y=-$\frac{12}{x}$或y=-$\frac{119}{25x}$.
如图,反比例函数y=$\frac{k}{x}$(x<0)的图象经过平行四边形OABC的两个顶点B,C,若点A的坐标为(1,2),AB=$\sqrt{5}$BC,则反比例函数的解析式为y=-$\frac{12}{x}$或y=-$\frac{119}{25x}$.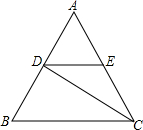 如图,△ABC是等边三角形,CD是∠ACB的平分线,过点D作BC的平行线交AC于点E,已知△ABC的边长为4,则EC的边长是2.
如图,△ABC是等边三角形,CD是∠ACB的平分线,过点D作BC的平行线交AC于点E,已知△ABC的边长为4,则EC的边长是2.