题目内容
4.先化简,再求值:($\frac{{x}^{2}-1}{{x}^{2}-2x+1}$+$\frac{1-x}{x+1}$)÷$\frac{x}{x-1}$,其中x=$\sqrt{3}$-4.分析 先计算括号,能约分的先约分,后计算乘法,最后代入即可.
解答 解:原式=[$\frac{(x+1)(x-1)}{(x-1)^{2}}$+$\frac{1-x}{x+1}$]•$\frac{x-1}{x}$
=($\frac{x+1}{x-1}$+$\frac{1-x}{x+1}$)•$\frac{x-1}{x}$
=$\frac{(x+1)^{2}-(x-1)^{2}}{(x+1)(x-1)}$•$\frac{x-1}{x}$
=$\frac{4}{x+1}$,
∵x=$\sqrt{3}$-4,
∴原式=$\frac{4}{\sqrt{3}-3}$=-2-$\frac{2\sqrt{3}}{3}$.
点评 本题考查分式的约分化简、因式分解等知识,解题的关键是熟练掌握分式的混合运算法则,注意简便运算,属于中考常考题型.

练习册系列答案
相关题目
19.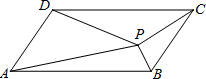 如图,平行四边形ABCD中,P是形内任意一点,△ABP,△BCP,△CDP,△ADP的面积分别为S1,S2,S3,S4,则一定成立的是( )
如图,平行四边形ABCD中,P是形内任意一点,△ABP,△BCP,△CDP,△ADP的面积分别为S1,S2,S3,S4,则一定成立的是( )
 如图,平行四边形ABCD中,P是形内任意一点,△ABP,△BCP,△CDP,△ADP的面积分别为S1,S2,S3,S4,则一定成立的是( )
如图,平行四边形ABCD中,P是形内任意一点,△ABP,△BCP,△CDP,△ADP的面积分别为S1,S2,S3,S4,则一定成立的是( )| A. | S1+S2=S3+S4 | B. | S1+S2>S3+S4 | C. | S1+S3=S2+S4 | D. | S1+S2<S3+S4 |
 已知:如图,在四边形ABCD中,AD∥BC,∠ABC=90°,点E是DC的中点,过点E作DC的垂线交AB于点P,交CB的延长线于点M,点F在线段ME上,且满足CF=AD,MF=MA.
已知:如图,在四边形ABCD中,AD∥BC,∠ABC=90°,点E是DC的中点,过点E作DC的垂线交AB于点P,交CB的延长线于点M,点F在线段ME上,且满足CF=AD,MF=MA.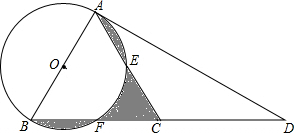 如图,在△ABC中,AC=BC,延长BC到点D,使CD=CB,连接AD,以AB为直径作⊙O,分别交AC、BC于点E、F
如图,在△ABC中,AC=BC,延长BC到点D,使CD=CB,连接AD,以AB为直径作⊙O,分别交AC、BC于点E、F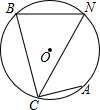 如图,⊙O是△BCN的外接圆,弦AC⊥BC,点N是$\widehat{AB}$的中点,∠BNC=60°,求$\frac{BN}{BC}$的值.
如图,⊙O是△BCN的外接圆,弦AC⊥BC,点N是$\widehat{AB}$的中点,∠BNC=60°,求$\frac{BN}{BC}$的值.