题目内容
18.(1)计算:9$\sqrt{3}$+7$\sqrt{12}$-5$\sqrt{48}$+2$\sqrt{\frac{1}{3}}$(2)先化简,再求值:$\frac{a-b}{a}$÷(a-$\frac{2ab-{b}^{2}}{a}$),其中a=$\sqrt{3}$+1,b=$\sqrt{3}$-1.
分析 (1)先把式化为最减二次根式的形式,再合并同类项即可;
(2)先根据分式混合运算的法则把原式进行化简,再a,b的值代入进行计算即可.
解答 解:(1)原式=9$\sqrt{3}$+14$\sqrt{3}$-20$\sqrt{3}$+$\frac{2\sqrt{3}}{3}$
=$\frac{11\sqrt{3}}{3}$;
(2)原式=$\frac{a-b}{a}$÷$\frac{{a}^{2}-2ab+{b}^{2}}{a}$
=$\frac{a-b}{a}$•$\frac{a}{(a-b)^{2}}$
=$\frac{1}{a-b}$,
当a=$\sqrt{3}$+1,b=$\sqrt{3}$-1时,原式=$\frac{1}{(\sqrt{3}+1)-(\sqrt{3}-1)}$=$\frac{1}{2}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
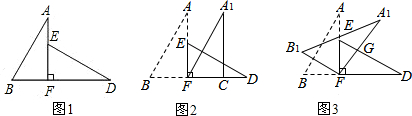
13. 如图,在△ABC中,∠BAC=90°,AB=AC,AD是经过A点的一条直线,且B、C在AD的两侧,BD⊥AD于D,CE⊥AD于E,交AB于点F,CE=10,BD=4,则DE的长为( )
如图,在△ABC中,∠BAC=90°,AB=AC,AD是经过A点的一条直线,且B、C在AD的两侧,BD⊥AD于D,CE⊥AD于E,交AB于点F,CE=10,BD=4,则DE的长为( )
 如图,在△ABC中,∠BAC=90°,AB=AC,AD是经过A点的一条直线,且B、C在AD的两侧,BD⊥AD于D,CE⊥AD于E,交AB于点F,CE=10,BD=4,则DE的长为( )
如图,在△ABC中,∠BAC=90°,AB=AC,AD是经过A点的一条直线,且B、C在AD的两侧,BD⊥AD于D,CE⊥AD于E,交AB于点F,CE=10,BD=4,则DE的长为( )| A. | 6 | B. | 5 | C. | 4 | D. | 8 |
3.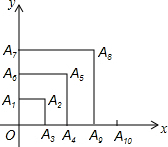 如图,有一系列有规律的点,它们分别是以O为顶点,边长为正整数的正方形的顶点:A1(0,1),A2(1,1),A3(1,0),A4(2,0),A5(2,2),A6(0,2),A7(0,3),A8(3,3),…,依此规律,点A2016的坐标为( )
如图,有一系列有规律的点,它们分别是以O为顶点,边长为正整数的正方形的顶点:A1(0,1),A2(1,1),A3(1,0),A4(2,0),A5(2,2),A6(0,2),A7(0,3),A8(3,3),…,依此规律,点A2016的坐标为( )
 如图,有一系列有规律的点,它们分别是以O为顶点,边长为正整数的正方形的顶点:A1(0,1),A2(1,1),A3(1,0),A4(2,0),A5(2,2),A6(0,2),A7(0,3),A8(3,3),…,依此规律,点A2016的坐标为( )
如图,有一系列有规律的点,它们分别是以O为顶点,边长为正整数的正方形的顶点:A1(0,1),A2(1,1),A3(1,0),A4(2,0),A5(2,2),A6(0,2),A7(0,3),A8(3,3),…,依此规律,点A2016的坐标为( )| A. | (0,672) | B. | (671,671) | C. | (672,672) | D. | (672,0) |
10.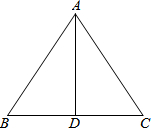 如图,在△ABC中,AB=AC,AD是BC边上中线.若AB=10,AD=8,则△ABC的周长是( )
如图,在△ABC中,AB=AC,AD是BC边上中线.若AB=10,AD=8,则△ABC的周长是( )
 如图,在△ABC中,AB=AC,AD是BC边上中线.若AB=10,AD=8,则△ABC的周长是( )
如图,在△ABC中,AB=AC,AD是BC边上中线.若AB=10,AD=8,则△ABC的周长是( )| A. | 26 | B. | 28 | C. | 32 | D. | 36 |
8.方程3x2=0和方程5x2=6x的根( )
| A. | 都是x=0 | B. | 有一个相同,x=0 | C. | 都不相同 | D. | 以上都不正确 |
 用一段长24m的篱笆围成一个一边靠墙的矩形菜园,墙长为15m,这个矩形长、宽各为多少时,菜园面积最大,最大面积是多少?
用一段长24m的篱笆围成一个一边靠墙的矩形菜园,墙长为15m,这个矩形长、宽各为多少时,菜园面积最大,最大面积是多少?