题目内容
10.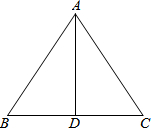 如图,在△ABC中,AB=AC,AD是BC边上中线.若AB=10,AD=8,则△ABC的周长是( )
如图,在△ABC中,AB=AC,AD是BC边上中线.若AB=10,AD=8,则△ABC的周长是( )| A. | 26 | B. | 28 | C. | 32 | D. | 36 |
分析 由等腰三角形的三线合一性质得出AD⊥BC,BD=CD=$\frac{1}{2}$BC,由勾股定理求出BD,得出BC,即可得出结果.
解答 解:∵AB=AC,AD是BC边上中线,
∴AD⊥BC,BD=CD=$\frac{1}{2}$BC,
∴BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6,
∴BC=2BD=12,
∴△ABC的周长=AB+AC+BC=10+10+12=32;
故选:C.
点评 本题考查了等腰三角形的性质、勾股定理;熟练掌握等腰三角形的三线合一性质,由勾股定理求出BD是解决问题的关键.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
15.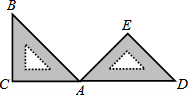 如图,将含45°的直角三角板ABC绕着点A顺时针旋转到△ADE处(点C,A,D在一条直线上),则这次旋转的旋转角为( )
如图,将含45°的直角三角板ABC绕着点A顺时针旋转到△ADE处(点C,A,D在一条直线上),则这次旋转的旋转角为( )
 如图,将含45°的直角三角板ABC绕着点A顺时针旋转到△ADE处(点C,A,D在一条直线上),则这次旋转的旋转角为( )
如图,将含45°的直角三角板ABC绕着点A顺时针旋转到△ADE处(点C,A,D在一条直线上),则这次旋转的旋转角为( )| A. | 45° | B. | 90° | C. | 135° | D. | 180° |
2. 如图,已知△ABC中,∠C=90°,AC=BC=2$\sqrt{2}$,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,则C′B的长为( )
如图,已知△ABC中,∠C=90°,AC=BC=2$\sqrt{2}$,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,则C′B的长为( )
 如图,已知△ABC中,∠C=90°,AC=BC=2$\sqrt{2}$,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,则C′B的长为( )
如图,已知△ABC中,∠C=90°,AC=BC=2$\sqrt{2}$,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,则C′B的长为( )| A. | 2$\sqrt{3}$-2 | B. | $\sqrt{3}$ | C. | 4-2$\sqrt{2}$ | D. | 2 |
20.下列运算中,正确的是( )
| A. | ($\sqrt{2}$+1)($\sqrt{2}$-1)=3 | B. | $\sqrt{6}$÷$\sqrt{3}$=$\sqrt{2}$ | C. | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{6}$ | D. | 2$\sqrt{3}$+3$\sqrt{3}$=6$\sqrt{3}$ |
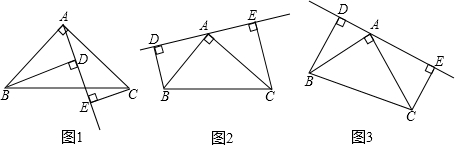
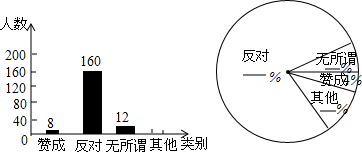
 ,剩下的工程由乙队单独做,也正好如期完工.一同学设规定的工期为x天,根据题意列出方程:
,剩下的工程由乙队单独做,也正好如期完工.一同学设规定的工期为x天,根据题意列出方程: