题目内容
12.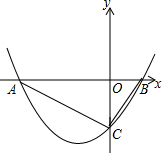 如图,已知抛物线y=$\frac{1}{2}$x2+bx+c与x轴交于A(-4,0),B(1,0)两点,与y轴交于C点,则△ABC的面积是5.
如图,已知抛物线y=$\frac{1}{2}$x2+bx+c与x轴交于A(-4,0),B(1,0)两点,与y轴交于C点,则△ABC的面积是5.
分析 由待定系数法求出抛物线的解析式,得出OC的长,即可得出△ABC的面积.
解答 解:根据题意得:OA=4,OB=1,$\left\{\begin{array}{l}{8-4b+c=0}\\{\frac{1}{2}+b+c=0}\end{array}\right.$,
解得:b=$\frac{3}{2}$,c=-2,
∴y═$\frac{1}{2}$x2+$\frac{3}{2}$x-2,
当x=0时,y=-2,
∴C(0,-2),
∴OC=2,
∵OA+OB=5,
∴△ABC的面积=$\frac{1}{2}$AB•OC=$\frac{1}{2}$×5×2=5.
故答案为:5.
点评 本题考查了抛物线与x轴的交点、待定系数法求抛物线的解析式、三角形面积的计算;用待定系数法求出抛物线的解析式是解决问题的关键.

练习册系列答案
相关题目
20.表一是甲、乙两名学生这学期的数学测试成绩一览表(单位:分)
表一
已知甲平时成绩的平均分是98分,乙平时成绩的众数是93分,请你完成下列问题:
(1)求表中m和n的值
(2)请求出甲、乙两名学生平时成绩的平均数,中位数、众数和方差,并填写表二
表二
(3)学校规定:学生平时成绩的平均数、期中成绩、期末成绩三项分别按40%、20%、40%的比例计入学期总评成绩,如果总评成绩不少以90分,平时成绩的平均分和期中成绩不变,那么,这两名学生的期末成绩至少应是多少?
表一
| 测试 类别 | 平时成绩 | 期中 | 期末 | ||||
| 测试1 | 测试2 | 测试3 | 测试4 | 测试5 | |||
| 甲 | m | 99 | 100 | 99 | 98 | 96 | 95 |
| 乙 | 90 | 93 | 94 | n | 95 | 92 | 98 |
(1)求表中m和n的值
(2)请求出甲、乙两名学生平时成绩的平均数,中位数、众数和方差,并填写表二
表二
| 学生 | 平均数 | 中位数 | 众数 | 方差 |
| 甲 | 98 | 99 | 99 | 4.4 |
| 乙 | 93 | 93 | 93 | 2.8 |
4. 下列条件不能够证明a∥b的是( )
下列条件不能够证明a∥b的是( )
 下列条件不能够证明a∥b的是( )
下列条件不能够证明a∥b的是( )| A. | ∠2+∠3=180° | B. | ∠1=∠4 | C. | ∠2+∠4=180° | D. | ∠2=∠3 |
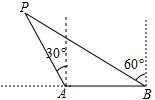 如图,海上有一小岛P,在他周围7海里内有暗礁,一艘轮船以15海里/时的速度由东向西方向航行至B点处测得小岛P在它北偏西60°的方向上,继续向西航行40分钟到达A处,又测得小岛P在它的北偏西30°方向上,如果货轮不改变方向能否继续航行?
如图,海上有一小岛P,在他周围7海里内有暗礁,一艘轮船以15海里/时的速度由东向西方向航行至B点处测得小岛P在它北偏西60°的方向上,继续向西航行40分钟到达A处,又测得小岛P在它的北偏西30°方向上,如果货轮不改变方向能否继续航行?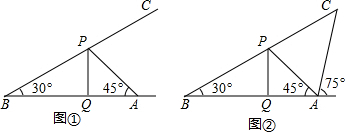
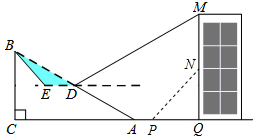 如图,斜坡AB长130米,坡度i=1:2.4,BC⊥AC,现计划在斜坡中点D处挖去部分坡体修建一个平行于水平线CA的平台DE和一条新的斜坡BE.
如图,斜坡AB长130米,坡度i=1:2.4,BC⊥AC,现计划在斜坡中点D处挖去部分坡体修建一个平行于水平线CA的平台DE和一条新的斜坡BE.