题目内容
 如图,在四边形ABCD中,AB=AD=6cm,CB=CD=8cm,且∠B=90°,该四边形存在内切圆吗?如果存在,请计算内切圆的半径.
如图,在四边形ABCD中,AB=AD=6cm,CB=CD=8cm,且∠B=90°,该四边形存在内切圆吗?如果存在,请计算内切圆的半径.考点:三角形的内切圆与内心
专题:存在型
分析:连结AD,作∠ABC的平分线交AC于O,作OH⊥BC于H,如图,易证得△ABC≌△ADC,则∠BAC=∠DAC,∠ACB=∠ACD,所以AC平分∠BAC和∠BCD,加上OB平分∠ABC,根据角平分线性质得到点O到四边形ABCD的各边的距离相等,则可判断四边形ABCD存在内切圆,内切圆的圆心为点O,半径为OH,接着证明△OBH为等腰直角三角形得到OH=BH,设OH=r,则BH=r,CH=8-r,然后证明△COH∽△CAB,利用相似比可计算出r.
解答:解:存在.
连接AC,作∠ABC的平分线交AC于O,作OH⊥BC于H,如图,
在△ABC和△ADC中,
,
∴△ABC≌△ADC,
∴∠BAC=∠DAC,∠ACB=∠ACD,
∴AC平分∠BAD和∠BCD,
∵OB平分∠ABC,
∴点O到四边形ABCD的各边的距离相等,
∴四边形ABCD存在内切圆,内切圆的圆心为点O,半径为OH,
∵∠ABC=90°,
∴∠OBH=45°,
∴△OBH为等腰直角三角形,
∴OH=BH,
设OH=r,则BH=r,CH=8-r,
∵OH∥AB,
∴△COH∽△CAB,
∴
=
,即
=
,
∴r=
,
即四边形ABCD的内切圆的半径为
.
连接AC,作∠ABC的平分线交AC于O,作OH⊥BC于H,如图,

在△ABC和△ADC中,
|
∴△ABC≌△ADC,
∴∠BAC=∠DAC,∠ACB=∠ACD,
∴AC平分∠BAD和∠BCD,
∵OB平分∠ABC,
∴点O到四边形ABCD的各边的距离相等,
∴四边形ABCD存在内切圆,内切圆的圆心为点O,半径为OH,
∵∠ABC=90°,
∴∠OBH=45°,
∴△OBH为等腰直角三角形,
∴OH=BH,
设OH=r,则BH=r,CH=8-r,
∵OH∥AB,
∴△COH∽△CAB,
∴
| OH |
| AB |
| CH |
| CB |
| r |
| 6 |
| 8-r |
| 8 |
∴r=
| 24 |
| 7 |
即四边形ABCD的内切圆的半径为
| 24 |
| 7 |
点评:本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形的内心就是三角形三个内角角平分线的交点.也考查了角平分线的性质和相似三角形的判定与性质.

练习册系列答案
相关题目
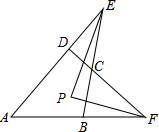 四边形ABCD中,AD、BC的延长线交于E,AB、DC的延长线交于F,∠AEB、∠AFD的平分线交于点P,∠A=44°,∠BCD=136°.
四边形ABCD中,AD、BC的延长线交于E,AB、DC的延长线交于F,∠AEB、∠AFD的平分线交于点P,∠A=44°,∠BCD=136°.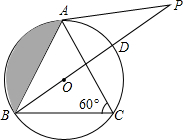 如图,在△ABC中,∠C=60°,⊙O是△ABC的外接圆,点P在直径BD的延长线上,且AB=AP.
如图,在△ABC中,∠C=60°,⊙O是△ABC的外接圆,点P在直径BD的延长线上,且AB=AP. 如图,AB∥CD,直线MN与AB、CD分别交于点E、F,∠AEM=2∠MEB,求∠DFN的度数.
如图,AB∥CD,直线MN与AB、CD分别交于点E、F,∠AEM=2∠MEB,求∠DFN的度数.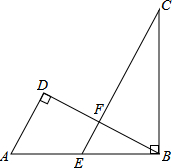 如图,在△ABD中,∠D=90°,点E是AB中点,BC⊥AB,且EC∥AD交BD于点F,若AB=4,BC=2
如图,在△ABD中,∠D=90°,点E是AB中点,BC⊥AB,且EC∥AD交BD于点F,若AB=4,BC=2