题目内容
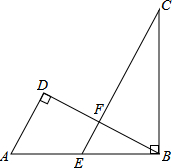 如图,在△ABD中,∠D=90°,点E是AB中点,BC⊥AB,且EC∥AD交BD于点F,若AB=4,BC=2
如图,在△ABD中,∠D=90°,点E是AB中点,BC⊥AB,且EC∥AD交BD于点F,若AB=4,BC=2| 2 |
考点:相似三角形的判定与性质,勾股定理
专题:
分析:首先利用勾股定理求出CE的长,由已知条件易证△ABD∽△ECB,根据相似三角形的性质可求出AD的长,因为EC∥AD,E为AB中点,所以EF为△ADB的中位线,进而可求出EF的长.
解答:解:∵BC⊥AB,
∴∠EBC=90°,
∵AB=4,点E是AB中点,
∴BE=2,
∴CE=
=2
,
∴∠D=∠EBC=90°,
∵EC∥AD交BD于点F,
∴∠A=∠CEB,
∴△ABD∽△ECB,
∴AD:BE=AB:CE,
∵AB=4,CE=2
,
∴AD:2=4:2
,
∴AD=
,
又∵因为EC∥AD,E为AB中点,
∴EF为△ADB的中位线,
∴EF=
AD=
,
故答案为:
.

∴∠EBC=90°,
∵AB=4,点E是AB中点,
∴BE=2,
∴CE=
| BC2+BE2 |
| 3 |
∴∠D=∠EBC=90°,
∵EC∥AD交BD于点F,
∴∠A=∠CEB,
∴△ABD∽△ECB,
∴AD:BE=AB:CE,
∵AB=4,CE=2
| 3 |
∴AD:2=4:2
| 3 |
∴AD=
4
| ||
| 3 |
又∵因为EC∥AD,E为AB中点,
∴EF为△ADB的中位线,
∴EF=
| 1 |
| 2 |
2
| ||
| 3 |
故答案为:
2
| ||
| 3 |
点评:本题考查了相似三角形的判定和性质、勾股定理的运用以及三角形中位线的判定和性质,题目的综合性较强,难度中等.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
 如图,在四边形ABCD中,AB=AD=6cm,CB=CD=8cm,且∠B=90°,该四边形存在内切圆吗?如果存在,请计算内切圆的半径.
如图,在四边形ABCD中,AB=AD=6cm,CB=CD=8cm,且∠B=90°,该四边形存在内切圆吗?如果存在,请计算内切圆的半径.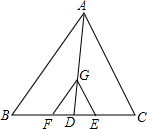 如图,在△ABC中,AD是中线,G是AD上一点,AG=2GD,CF∥AB,CE∥AC,分别交BC于点F、E.
如图,在△ABC中,AD是中线,G是AD上一点,AG=2GD,CF∥AB,CE∥AC,分别交BC于点F、E.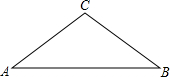 如图,△ABC中,BC=5,AC=5,AB=8.
如图,△ABC中,BC=5,AC=5,AB=8. 如图,在四边形ABCD中,AB=BC,AD=7,∠ADC=∠CBA=90°,tanA=2,求CD的长.
如图,在四边形ABCD中,AB=BC,AD=7,∠ADC=∠CBA=90°,tanA=2,求CD的长.