题目内容
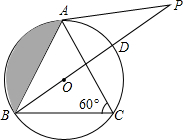 如图,在△ABC中,∠C=60°,⊙O是△ABC的外接圆,点P在直径BD的延长线上,且AB=AP.
如图,在△ABC中,∠C=60°,⊙O是△ABC的外接圆,点P在直径BD的延长线上,且AB=AP.(1)求证:PA是⊙O的切线;
(2)若AB=2
| 3 |
考点:切线的判定,扇形面积的计算
专题:
分析:(1)如图,连接OA;证明∠OAP=90°,即可解决问题.
(2)如图,作辅助线;求出OM=1,OA=2;求出△AOB、扇形AOB的面积,即可解决问题.
(2)如图,作辅助线;求出OM=1,OA=2;求出△AOB、扇形AOB的面积,即可解决问题.
解答: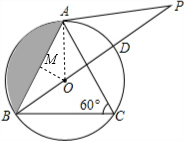 解:(1)如图,连接OA;
解:(1)如图,连接OA;
∵∠C=60°,
∴∠AOB=120°;而OA=OB,
∴∠OAB=∠OBA=30°;而AB=AP,
∴∠P=∠ABO=30°;
∵∠AOB=∠OAP+∠P,
∴∠OAP=120°-30°=90°,
∴PA是⊙O的切线.
(2)如图,过点O作OM⊥AB,则AM=BM=
,
∵tan30°=
,sin30°=
,
∴OM=1,OA=2;
∴S△AOB=
×AB•OM=
×2
×1=
,
S扇形OAB=
=
,
∴图中阴影部分的面积=
-
.
 解:(1)如图,连接OA;
解:(1)如图,连接OA;∵∠C=60°,
∴∠AOB=120°;而OA=OB,
∴∠OAB=∠OBA=30°;而AB=AP,
∴∠P=∠ABO=30°;
∵∠AOB=∠OAP+∠P,
∴∠OAP=120°-30°=90°,
∴PA是⊙O的切线.
(2)如图,过点O作OM⊥AB,则AM=BM=
| 3 |
∵tan30°=
| OM |
| AM |
| OM |
| AO |
∴OM=1,OA=2;
∴S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
S扇形OAB=
| 120π•22 |
| 360 |
| 4π |
| 3 |
∴图中阴影部分的面积=
| 4π |
| 3 |
| 3 |
点评:该题主要考查了切线的判定、扇形的面积公式及其应用问题;解题的关键是作辅助线;灵活运用圆周角定理及其推论、垂径定理等几何知识点来分析、判断、解答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
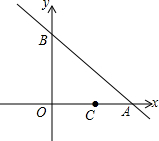 已知,如图,函数y=-x+2的图象与x轴,y轴分别相交于点A,B,一直线L经过点B、点C,将△AOB的面积分成相等的两部分.
已知,如图,函数y=-x+2的图象与x轴,y轴分别相交于点A,B,一直线L经过点B、点C,将△AOB的面积分成相等的两部分.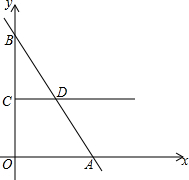 如图,在平面直角坐标系中,直线l:y=kx+20与x轴、y轴分别交于点A、B,OB=2AO,过点C(0,8)做射线CD交直线l于点D,且CD∥x轴.动点P从点O出发沿y轴的正半轴向点B运动,速度为每秒2个单位长度.过点P做x轴的平行线交直线l于点Q.
如图,在平面直角坐标系中,直线l:y=kx+20与x轴、y轴分别交于点A、B,OB=2AO,过点C(0,8)做射线CD交直线l于点D,且CD∥x轴.动点P从点O出发沿y轴的正半轴向点B运动,速度为每秒2个单位长度.过点P做x轴的平行线交直线l于点Q. 如图,在四边形ABCD中,AB=AD=6cm,CB=CD=8cm,且∠B=90°,该四边形存在内切圆吗?如果存在,请计算内切圆的半径.
如图,在四边形ABCD中,AB=AD=6cm,CB=CD=8cm,且∠B=90°,该四边形存在内切圆吗?如果存在,请计算内切圆的半径.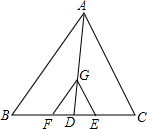 如图,在△ABC中,AD是中线,G是AD上一点,AG=2GD,CF∥AB,CE∥AC,分别交BC于点F、E.
如图,在△ABC中,AD是中线,G是AD上一点,AG=2GD,CF∥AB,CE∥AC,分别交BC于点F、E.