题目内容
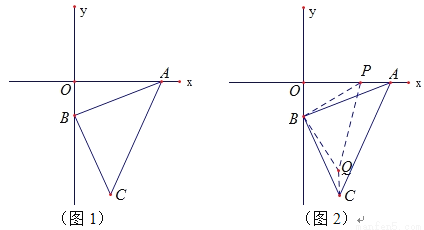
如图,已知A(3，0),B(0，-1)，连接AB,过B点作AB的垂线段,使BA=BC,连接AC.
(1)如图1，求C点坐标；
(2)如图2,若P点从A点出发,沿x轴向左平移,连接BP,作等腰直角三角形△BPQ,连接CQ.求证:PA=CQ.
(3)在(2)的条件下,若C、P、Q三点共线,求此时P点坐标及∠APB的度数.
练习册系列答案
相关题目
题目内容
如图,已知A(3，0),B(0，-1)，连接AB,过B点作AB的垂线段,使BA=BC,连接AC.
(1)如图1，求C点坐标；
(2)如图2,若P点从A点出发,沿x轴向左平移,连接BP,作等腰直角三角形△BPQ,连接CQ.求证:PA=CQ.
(3)在(2)的条件下,若C、P、Q三点共线,求此时P点坐标及∠APB的度数.
中， 
为
边上一点， 
为
边上一点， 
与
相似，己知
， 
， 
，则
__________．
）．
，⊙O的半径为1，点P是AB边上的动点，过点P作⊙O的一条切线PQ（点Q为切点），则切线PQ的最小值为（ ）．
D．2
的内切圆，点
分别为边
上的点，且
为⊙I的切线，若
的周长为21， 
边的长为6，则
的周长为（ ）
+2b﹣1)(3
﹣2b+1)
－1）（
＋1）2的结果是（ ）
＋1 B. 3（
－1） C. 1 D. －1