题目内容
2.如图,在矩形ABCD中,AB的长度为a(4<a<6),BC的长度为6,将矩形纸片按下图顺序折叠.(1)C′D′的长度为3a-12(用含a的代数式表示);
(2)四边形C′D′EF面积的最大值为3.
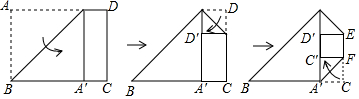
分析 (1)由轴对称可以得出A′B=AB=a,求得A′C=6-a.由轴对称的性质得到A′C′=6-a,于是得到结论;
(2)由折叠的性质可知,四边形C′D′EF是矩形,由(1)知C′D′=3a-12,于是得到C′F=A′C′=6-a,根据矩形的面积公式得到四边形C′D′EF面积=(3a-12)•(6-a)=-3a2+30a-72=-3(a-5)2+3,于是得到结论.
解答  解:(1)由轴对称可以得出A′B=AB=a,
解:(1)由轴对称可以得出A′B=AB=a,
∵BC=6,
∴A′C=6-a.
由轴对称可以得出A′C′=6-a,
∴C′D′=a-2(6-a),
∴C′D′=3a-12.
故答案为:3a-12;
(2)由折叠的性质可知,四边形C′D′EF是矩形,
∵C′D′=3a-12,C′F=A′C′=6-a,
∴四边形C′D′EF面积=(3a-12)•(6-a)=-3a2+30a-72=-3(a-5)2+3,
∴当a=5时,四边形C′D′EF面积的最大值为3,
故答案为:3.
点评 本题考查了轴对称的运用,代数式的运用,折叠问题在实际问题中的运用,矩形的性质,二次函数的最值,解答本题时利用折叠问题抓住在折叠变化中不变的线段是解答本题的关键.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
17.已知函数y=(m+1)x+m的函数值y随自变量x的增大而减小,那么m的取值范围是( )
| A. | m>-1 | B. | m<-1 | C. | m<1 | D. | m<0 |
12. 如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(2,2),第2次接着运动到点(4,0),第3次接着运动到点(6,1),…,按这样的运动规律,经过第72次运动后,动点P的坐标是( )
如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(2,2),第2次接着运动到点(4,0),第3次接着运动到点(6,1),…,按这样的运动规律,经过第72次运动后,动点P的坐标是( )
 如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(2,2),第2次接着运动到点(4,0),第3次接着运动到点(6,1),…,按这样的运动规律,经过第72次运动后,动点P的坐标是( )
如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(2,2),第2次接着运动到点(4,0),第3次接着运动到点(6,1),…,按这样的运动规律,经过第72次运动后,动点P的坐标是( )| A. | (144,0) | B. | (142,2) | C. | (72,0) | D. | (142,1) |
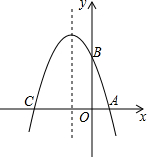 如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴交于A、C两点,与y轴交于点B,且OA=1,OC=4.
如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴交于A、C两点,与y轴交于点B,且OA=1,OC=4.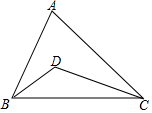 如图,在△ABC中,∠A=70°,D是△ABC内一点,若∠ABD=30°,∠ACD=25°,则∠BDC=125°.
如图,在△ABC中,∠A=70°,D是△ABC内一点,若∠ABD=30°,∠ACD=25°,则∠BDC=125°.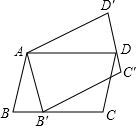 如图,?ABCD绕点A逆时针旋转45°,得到?AB′C′D′(点B′与B是对应点,点C′与点C是对应点,点D′与点D是对应点).点B′恰好落在BC边上,则∠C=112.5°.
如图,?ABCD绕点A逆时针旋转45°,得到?AB′C′D′(点B′与B是对应点,点C′与点C是对应点,点D′与点D是对应点).点B′恰好落在BC边上,则∠C=112.5°.