题目内容
10.已知方程组$\left\{\begin{array}{l}{x+3y=2n-1}\\{2x-y=m+1}\end{array}\right.$的解x,y满足条件:-1≤x≤1,1≤y≤2,求m2+n2的取值范围.分析 先把x、y的值用m、n表示出来,再代入-1≤x≤1,1≤y≤2即可求出m、n的取值范围,进一步得出m2+n2的取值范围.
解答 解:$\left\{\begin{array}{l}{x+3y=2n-1}\\{2x-y=m+1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=\frac{3m+2n+2}{7}}\\{y=\frac{4n-m-3}{7}}\end{array}\right.$,
∵-1≤x≤1,1≤y≤2,
∴$\left\{\begin{array}{l}{-1≤\frac{3m+2n+2}{7}≤1}\\{1≤\frac{4n-m-3}{7}≤2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{-5≤m≤0}\\{\frac{3}{2}≤n≤4}\end{array}\right.$,
∴m2+n2的最小值为$\frac{9}{4}$,m2+n2的最大值为41.
点评 本题考查的是解二元一次方程组及解一元一次不等式,解答此题的关键是先把m、n当作已知表示出x、y的值,即可得到关于m、n的二元一次不等式组,再根据解二元一次不等式组的方法求解.

练习册系列答案
相关题目
1.已知二次函数y1=ax2+bx+c(b≠c)图象的最高点坐标为(-2,4),则一次函数y2=(b-c)x+b2-4ac图象可能在( )
| A. | 一、二、三象限 | B. | 一、二、四象限 | C. | 一、三、四象限 | D. | 二、三、四象限 |
20.方程3x+2=2x-1的解为( )
| A. | x=-3 | B. | x=-1 | C. | x=1 | D. | x=3 |
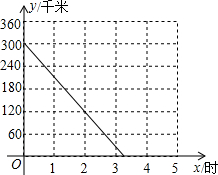 A、B两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条公路两端的入口处驶入,并始终在高速公路上正常行驶.甲车驶住B城,乙车驶往A城,甲车在行驶过程中速度始终不变,甲车距B城高速公路入口处的距离y(km)与行驶时间x(h)之间的关系如图.
A、B两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条公路两端的入口处驶入,并始终在高速公路上正常行驶.甲车驶住B城,乙车驶往A城,甲车在行驶过程中速度始终不变,甲车距B城高速公路入口处的距离y(km)与行驶时间x(h)之间的关系如图.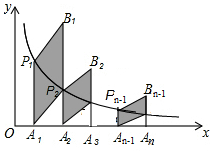 如图,分别过反比例函数y=$\frac{3}{x}$(x>0)图象上的点P1(1,y1),P2(2,y2)…Pn(n,yn)作x轴的垂线,垂足分别为A1,A2,…An,连结A1P2,A2P3,…An-1Pn,再以A1P1,A1P2为一组邻边作平行四边形A1P1B1P2,以A2P2,A2P3为邻边作平行四边形A2P2B2P3,以此类推,则B1的纵坐标为$\frac{9}{2}$,Bn的纵坐标为$\frac{6n+3}{n(n+1)}$(用含n的代数式表示)
如图,分别过反比例函数y=$\frac{3}{x}$(x>0)图象上的点P1(1,y1),P2(2,y2)…Pn(n,yn)作x轴的垂线,垂足分别为A1,A2,…An,连结A1P2,A2P3,…An-1Pn,再以A1P1,A1P2为一组邻边作平行四边形A1P1B1P2,以A2P2,A2P3为邻边作平行四边形A2P2B2P3,以此类推,则B1的纵坐标为$\frac{9}{2}$,Bn的纵坐标为$\frac{6n+3}{n(n+1)}$(用含n的代数式表示)