题目内容
11.(1)解分式方程:$\frac{5}{x-1}$=$\frac{1}{x+3}$(2)已知$\frac{1}{x}$-$\frac{1}{y}$=5,求分式$\frac{-x+xy+y}{2x+7xy-2y}$的值.
分析 (1)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;
(2)已知等式整理得到y-x=5xy,原式变形后代入计算即可求出值.
解答 解:(1)方程两边同时乘以(x+3)(x-1)去分母得5(x+3)=x-1,
整理得:4x=-16,
解得:x=-4,
经检验:x=-4是方程的解,
方程的解是x=-4;
(2)由$\frac{1}{x}$-$\frac{1}{y}$=$\frac{y-x}{xy}$=5得:y-x=5xy,
则$\frac{-x+xy+y}{2x+7xy-2y}$=$\frac{y-x+xy}{-2(y-x)+7xy}$,
将 y-x=5xy 代入得:原式=$\frac{5xy+xy}{-2×5xy+7xy}$=$\frac{6xy}{-3xy}$=-2.
点评 此题考查了解分式方程,以及分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
1.已知二次函数y1=ax2+bx+c(b≠c)图象的最高点坐标为(-2,4),则一次函数y2=(b-c)x+b2-4ac图象可能在( )
| A. | 一、二、三象限 | B. | 一、二、四象限 | C. | 一、三、四象限 | D. | 二、三、四象限 |
20.方程3x+2=2x-1的解为( )
| A. | x=-3 | B. | x=-1 | C. | x=1 | D. | x=3 |
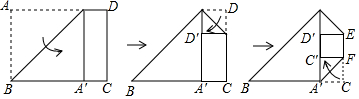
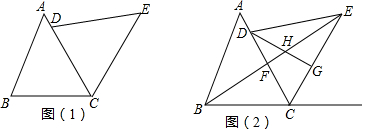
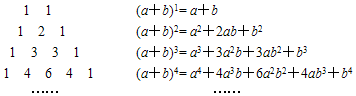
 如图,在正方形网格中,△ABC的三个顶点都在格点上,按要求解答下列问题:
如图,在正方形网格中,△ABC的三个顶点都在格点上,按要求解答下列问题: 如图,一次函数的图象经过点M,与x轴交于点A,与y轴交于点B,求S△AOB.
如图,一次函数的图象经过点M,与x轴交于点A,与y轴交于点B,求S△AOB.