Question

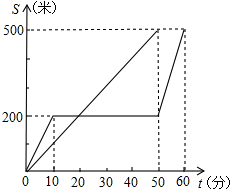“龟兔赛跑”是同学们熟悉的寓言故事．如图所示，表示了寓言中的龟、兔的路程S和时间t的关系（其中直线段表示乌龟，折线段表示兔子），请看图回答问题．
（1）赛跑中，兔子共睡了

 

分钟；
（2）乌龟在这次比赛中的平均速度是

 

米/分钟；
（3）乌龟比兔子早达到终点

 

分钟；
（4）求兔子最后冲刺时的函数关系式．
（5）乌龟与兔子之间距离不超过10米的时候的t的范围是

 

．

Answer 1

考点：一次函数的应用

专题：

分析：（1）由函数图象可以得出兔子睡觉的时间为50-10=40分钟；
（2）由路程÷速度=时间就可以求出结论；
（3）由函数图象可以得出乌龟比兔子早达到终点的时间为60-50=10分钟；
（4）设兔子最后冲刺时直线CD的函数关系式为y=kt+b，由待定系数法求出其解即可；
（5）设OA的解析式为y=k₁t，OB的解析式为y=k₂t，由待定系数法求出其解，再由函数的解析式建立不等式组，求出其解即可．

解答：解：（1）由题意，得
50-10=40，
故答案为：40；
（2）由题意，得
乌龟在这次比赛中的平均速度是：
500÷50=10．
故答案为10；
（3）由函数图象，得
乌龟比兔子早达到终点的时间为：
60-50=10分钟．
故答案为：10；
（4）兔子最后冲刺时直线CD的函数关系式为y=kt+b，由题意，得

200=50k+b 500=60k+b

，
解得：

k=30 t=-1300

，
∴y=30t-1300（50≤k≤60）；
（5）设OA的解析式为y₁=k₁t，OB的解析式为y₂=k₂t，由题意，得
200=10k₁，500=50k₂，
解得：k₁=20，k₂=10．
∴y₁=20t，y₂=10t．
20t-10t≤10，
t≤1，

200-10t≤10 10t-200≤10

，
解得：19≤t≤21．
故答案为：t≤1或19≤t≤21．

点评：本题考查了一次函数的解析式的运用，分段函数的运用，行程问题的数量关系的运用，一元一次不等式及不等式组的解法的运用，解答时求出一次函数的解析式是关键．