题目内容
 如图,正方形ABCD的边长为2,△ABE是等边三角形.
如图,正方形ABCD的边长为2,△ABE是等边三角形.(1)求∠ACE的度数.
(2)求AF的长.
考点:勾股定理,等边三角形的性质,正方形的性质
专题:
分析:(1)根据正方形的性质和等边三角形的性质可得∠CBE=30°,∠BCA=45°,根据等腰三角形的性质和三角形内角和定理可得∠BCE的度数,再根据角的和差关系即可求解;
(2)作FH⊥AB于H,设BH=x,则BF=2x,根据三角函数可得FH=
x=AH,可得AH的长,再根据勾股定理可得AF的长.
(2)作FH⊥AB于H,设BH=x,则BF=2x,根据三角函数可得FH=
| 3 |
解答: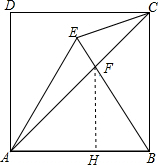 解:(1)∵△ABE是等边三角形,
解:(1)∵△ABE是等边三角形,
∴∠ABE=60°,
∴∠CBE=30°,
∵四边形ABCD是正方形,
∴BE=BC,∠BCA=45°,
∴∠BCE=(180°-30°)÷2=75°,
∴∠ACE=∠BCE-∠BCA=30°;
(2)作FH⊥AB于H,
设BH=x,则BF=2x,FH=
x=AH.
∴x+
x=2,
∴x=
-1,
∴AH=
(
-1),
AF=
AH=
(
-1)=3
-
.
 解:(1)∵△ABE是等边三角形,
解:(1)∵△ABE是等边三角形,∴∠ABE=60°,
∴∠CBE=30°,
∵四边形ABCD是正方形,
∴BE=BC,∠BCA=45°,
∴∠BCE=(180°-30°)÷2=75°,
∴∠ACE=∠BCE-∠BCA=30°;
(2)作FH⊥AB于H,
设BH=x,则BF=2x,FH=
| 3 |
∴x+
| 3 |
∴x=
| 3 |
∴AH=
| 3 |
| 3 |
AF=
| 2 |
| 6 |
| 3 |
| 2 |
| 6 |
点评:考查了正方形的性质,等边三角形的性质,等腰三角形的性质和三角形内角和定理,三角函数和勾股定理,关键是作出辅助线,构造直角三角形.

练习册系列答案
相关题目
 如图,AD∥EG,AD平分∠BAC,证明:∠E=∠1.
如图,AD∥EG,AD平分∠BAC,证明:∠E=∠1.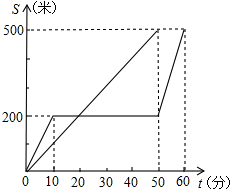 “龟兔赛跑”是同学们熟悉的寓言故事.如图所示,表示了寓言中的龟、兔的路程S和时间t的关系(其中直线段表示乌龟,折线段表示兔子),请看图回答问题.
“龟兔赛跑”是同学们熟悉的寓言故事.如图所示,表示了寓言中的龟、兔的路程S和时间t的关系(其中直线段表示乌龟,折线段表示兔子),请看图回答问题. 如图,一次函数y1=kx+b的图象与反比例函数y2=
如图,一次函数y1=kx+b的图象与反比例函数y2= 如图,将一条两边沿互相平行的纸带按如图折叠,设∠1=x,用含有x的代数式表示∠2,则∠2=
如图,将一条两边沿互相平行的纸带按如图折叠,设∠1=x,用含有x的代数式表示∠2,则∠2=