题目内容
(1)如图1,四边形ABCD是菱形,CE⊥AB交AB延长线于E,CF⊥AD交AD延长线于F,求证:CE=CF.
(2)已知:如图2,AB为⊙C的直径,PA、PC是⊙O的切线,A、C为切点,∠BAC=30°.若AB=2,求PA的长.

(2)已知:如图2,AB为⊙C的直径,PA、PC是⊙O的切线,A、C为切点,∠BAC=30°.若AB=2,求PA的长.

考点:切线的性质,菱形的性质
专题:
分析:(1)连接AC,根据菱形的性质可得AC平分∠DAE,再根据角平分线的性质可得CE=FC;
(2)由圆的切线的性质,得∠PAB=90°,结合∠BAC=30°得∠PAC=90°-30°=60°.由切线长定理得到PA=PC,得△PAC是等边三角形,从而可得∠P=60°;连结BC,根据直径所对的圆周角为直角,得到∠ACB=90°,结合Rt△ACB中AB=2且∠BAC=30°,得到AC=ABcos∠BAC=
.最后在等边△PAC中,可得PA=AC=
.
(2)由圆的切线的性质,得∠PAB=90°,结合∠BAC=30°得∠PAC=90°-30°=60°.由切线长定理得到PA=PC,得△PAC是等边三角形,从而可得∠P=60°;连结BC,根据直径所对的圆周角为直角,得到∠ACB=90°,结合Rt△ACB中AB=2且∠BAC=30°,得到AC=ABcos∠BAC=
| 3 |
| 3 |
解答:证明:(1)连接AC,

∵四边形ABCD为菱形,
∴AC平分∠DAC,
又∵CE⊥AB,CF⊥AD,
∴CE=CF;
解:(2)∵PA是⊙O的切线,AB为⊙O的直径,
∴PA⊥AB,即∠PAB=90°.
∵∠BAC=30°,∴∠PAC=90°-30°=60°.
又∵PA、PC切⊙O于点A、C,
∴PA=PC,可得△PAC是等边三角形,得∠P=60°.
如图,连结BC.

∵AB是直径,∠ACB=90°,
∴在Rt△ACB中,AB=2,∠BAC=30°,
可得AC=ABcos∠BAC=2×cos30°=
.
又∵△PAC是等边三角形,
∴PA=AC=
.

∵四边形ABCD为菱形,
∴AC平分∠DAC,
又∵CE⊥AB,CF⊥AD,
∴CE=CF;
解:(2)∵PA是⊙O的切线,AB为⊙O的直径,
∴PA⊥AB,即∠PAB=90°.
∵∠BAC=30°,∴∠PAC=90°-30°=60°.
又∵PA、PC切⊙O于点A、C,
∴PA=PC,可得△PAC是等边三角形,得∠P=60°.
如图,连结BC.

∵AB是直径,∠ACB=90°,
∴在Rt△ACB中,AB=2,∠BAC=30°,
可得AC=ABcos∠BAC=2×cos30°=
| 3 |
又∵△PAC是等边三角形,
∴PA=AC=
| 3 |
点评:此题考查菱形的性质、角平分线的性质以及圆的切线的性质定理、切线长定理、直径所对的圆周角、等边三角形的判定与性质和解直角三角形等知识,属于基础题.

练习册系列答案
相关题目

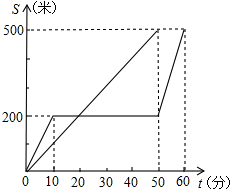 “龟兔赛跑”是同学们熟悉的寓言故事.如图所示,表示了寓言中的龟、兔的路程S和时间t的关系(其中直线段表示乌龟,折线段表示兔子),请看图回答问题.
“龟兔赛跑”是同学们熟悉的寓言故事.如图所示,表示了寓言中的龟、兔的路程S和时间t的关系(其中直线段表示乌龟,折线段表示兔子),请看图回答问题.