题目内容
15．
如图所示，有两棵树，一棵高AD=6米，另一棵高BC=2米，两树相距DC=8米，一只小鸟从一棵树的树梢B飞到另一棵树的树梢A，至少飞了4$\sqrt{5}$米．
分析 根据“两点之间线段最短”可知：小鸟沿着两棵树的树尖进行直线飞行，所行的路程最短，运用勾股定理可将两点之间的距离求出．
解答 解：两棵树的高度差为：AE=6-2=4m，间距为BE=DC=8m，
根据勾股定理可得：小鸟至少飞行的距离=$\sqrt{{8}^{2}+{4}^{2}}$=4$\sqrt{5}$（m）．
故答案为：4$\sqrt{5}$．
点评 本题主要考查了勾股定理的应用，解题的关键是将现实问题建立数学模型，运用数学知识进行求解．
练习册系列答案
相关题目
如图，在矩形ABCD中，M，N分别是AD，BC的中点，P，Q分别是BM，DN的中点
如图，C是线段BD上一点，分别以BC和CD为边长，在直线BD的同一侧作两个等边三角形，△ABC和△ECD，连接BE和AD，BE与AC交于点F，AD与CE交于点G．
如图，⊙P经过点A（0，$\sqrt{3}$）、O（0，0）、B（1，0），点C在第一象限的$\widehat{AB}$上，则∠BCO的度数为30°．
一天小强和爷爷去爬山，小强让爷爷先上山，然后追赶爷爷．图中两条线段分别表示小强和爷爷离开山脚的距离y（米）与爬山所用时间x（分）的关系（从小强开始爬山时计时），看图回答下列问题：
4．
如图，在平面直角坐标系中，直线y=$\frac{3}{4}$x+6交x轴于点A，交y轴于点B，D1是线段AB的中点，过D1作D1E1⊥x轴于E1，连接BE1交OD1于D2；过D2作D2E2⊥x轴于E2，连接BE2交OD1于D3；过D3作D3E3⊥x轴于E3，…，如此继续，可以依次得到点D4，D5，…，Dn，分别记△BD1E1，△BD2E2，△BD3E3，…，△BDnEn的面积为S1，S2，S3，…Sn．则Sn为（ ）
如图，在平面直角坐标系中，直线y=$\frac{3}{4}$x+6交x轴于点A，交y轴于点B，D1是线段AB的中点，过D1作D1E1⊥x轴于E1，连接BE1交OD1于D2；过D2作D2E2⊥x轴于E2，连接BE2交OD1于D3；过D3作D3E3⊥x轴于E3，…，如此继续，可以依次得到点D4，D5，…，Dn，分别记△BD1E1，△BD2E2，△BD3E3，…，△BDnEn的面积为S1，S2，S3，…Sn．则Sn为（ ）| A． | $\frac{24}{（n+1）^{2}}$ | B． | $\frac{12}{（n+1）^{2}}$ | C． | $\frac{24}{{n}^{2}}$ | D． | $\frac{12}{{n}^{2}}$ |
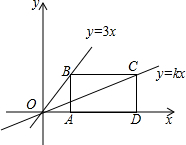如图，点B、C分别在两条直线y=3x和y=kx上，点A、D是x轴上两点，已知四边形ABCD是长方形，且BC=2AB，则k的值为$\frac{3}{7}$．