题目内容
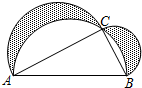 如图,班级美术课代表在办黑板报时设计了一个图案如图,在Rt△ABC中,∠C=90°,△ABC的面积为40cm2,在AB同侧分别以AB,BC,AC为直径作三个半圆,求阴影部分的面积.
如图,班级美术课代表在办黑板报时设计了一个图案如图,在Rt△ABC中,∠C=90°,△ABC的面积为40cm2,在AB同侧分别以AB,BC,AC为直径作三个半圆,求阴影部分的面积.考点:勾股定理
专题:
分析:根据阴影部分的面积等于以a、b为直径的两个半圆的面积加上△ABC的面积再减去以c为直径的半圆的面积列式并整理,再利用勾股定理解答.
解答:解:如图:

由图可知,阴影部分的面积
=
π(
b)2+
π(
a)2+S△ABC-
π(
c)2
=
(a2+b2-c2)+S△ABC,
在Rt△ABC中,a2+b2=c2,
故阴影部分的面积=S△ABC=40cm2.
故阴影部分的面积是40cm2.

由图可知,阴影部分的面积
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| π |
| 8 |
在Rt△ABC中,a2+b2=c2,
故阴影部分的面积=S△ABC=40cm2.
故阴影部分的面积是40cm2.
点评:本题考查了勾股定理,阴影部分的面积表示,观察图形,准确表示出阴影部分的面积是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
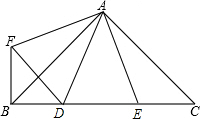 如图,在Rt△ABC中,AB=AC,∠BAC=90°,D、E为BC上两点,∠DAE=45°,过点A作AF⊥AE,且AF=AE,连接BF、EF.
如图,在Rt△ABC中,AB=AC,∠BAC=90°,D、E为BC上两点,∠DAE=45°,过点A作AF⊥AE,且AF=AE,连接BF、EF. 如图,在?ABCD中,点E,F在AD,BC上,且AE=CF,AF与BE交于点M,CE与DF交于点N,求证:四边形EMFN是平行四边形.
如图,在?ABCD中,点E,F在AD,BC上,且AE=CF,AF与BE交于点M,CE与DF交于点N,求证:四边形EMFN是平行四边形.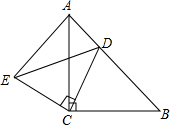 如图,△ACB和△ECD均为等腰直角三角形,∠ACB=∠ECD=90°,D在AB上.
如图,△ACB和△ECD均为等腰直角三角形,∠ACB=∠ECD=90°,D在AB上. (1)在数轴上把下列各数表示出来:
(1)在数轴上把下列各数表示出来: 如图,在Rt△DBC中,∠B=90°,∠D=30°,∠CAB=60°.且AD=6,求CD的长.
如图,在Rt△DBC中,∠B=90°,∠D=30°,∠CAB=60°.且AD=6,求CD的长. 已知平行四边形中空白部分的面积是77平方厘米,求图中阴影部分的面积.
已知平行四边形中空白部分的面积是77平方厘米,求图中阴影部分的面积. 如图,
如图,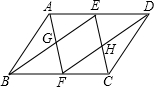 如图,已知?ABCD中,E、F分别为AD、BC的中点,AF与BE交于点G,CE和DF交于点H.说明:EG=HF.
如图,已知?ABCD中,E、F分别为AD、BC的中点,AF与BE交于点G,CE和DF交于点H.说明:EG=HF.