Question

5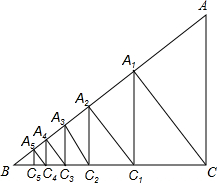．如图，已知直角△ACB，AC=3，BC=4，过直角顶点C作CA₁⊥AB，垂足为A₁，再过A₁作A₁C₁⊥BC，垂足为C₁；过C₁作C₁A₂⊥AB，垂足为A₂，再过A₂作A₂C₂⊥BC，垂足为C₂；…，这样一直做下去，得到一组线段A₁C₁，A₂C₂…，则线段A_nC_n为3×（$\frac{4}{5}$）²ⁿ．（用含有n的代数式表示）

Answer 1

分析 利用勾股定理求得AB的长，即可得sinA=$\frac{BC}{AB}$=$\frac{4}{5}$，在Rt△ACA₁中CA₁=ACsinA=3×$\frac{4}{5}$，由∠A+∠ACA₁=90°、∠CA₁C₁+∠ACA₁=90°得∠A=∠A₁CC₁，从而得出A₁C₁=CA₁•sinA=3×（$\frac{4}{5}$）²，同理得出A₂C₂=3×（$\frac{4}{5}$）⁴，据此可得出规律．

解答 解：∵Rt△ABC中，AC=3，BC=4，
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=5，
∴sinA=$\frac{BC}{AB}$=$\frac{4}{5}$，
∵CA₁⊥AB，
∴在Rt△ACA₁中，CA₁=ACsinA=3×$\frac{4}{5}$，
又∵∠A+∠ACA₁=90°，∠CA₁C₁+∠ACA₁=90°，
∴∠A=∠A₁CC₁，
∴A₁C₁=CA₁•sinA=3×（$\frac{4}{5}$）²，
同理可得A₂C₂=3×（$\frac{4}{5}$）⁴，
∴A_nC_n=3×（$\frac{4}{5}$）²ⁿ，
故答案为：3×（$\frac{4}{5}$）²ⁿ．

点评 本题主要考查了勾股定理、直角三角形的性质、运用锐角三角函数表示未知的边及分析归纳能力，关键是确定对应的锐角相等，确定边的对应关系，利用三角函数得出A₁C₁、A₂C₂的长，从而总结出规律．