题目内容
10. 如图,在△ABC中,AB=5,AC=3,AD、AE分别是它的角平分线和中线,过点C作CG⊥AD,垂足为点F,连接EF,则EF=1.
如图,在△ABC中,AB=5,AC=3,AD、AE分别是它的角平分线和中线,过点C作CG⊥AD,垂足为点F,连接EF,则EF=1.
分析 首先证明AG=AC,再证明EF是△BCG的中位线,根据EF=$\frac{1}{2}$BG即可解决问题.
解答 解:∵∠DAG=∠DAC,AD⊥AFC,
∴∠AFC=∠AFG=90°,
∴∠AGC+∠GAF=90°,∠ACG+∠CAF=90°,
∴∠AGC=∠ACG,
∴AG=AC=3,GF=FC,
∵BE=CE,
∴EF=$\frac{1}{2}$BG=$\frac{1}{2}$(AB-AG)=$\frac{1}{2}$×(5-3)=1,
故答案为1.
点评 本题考查三角形中位线定理、等腰三角形的判定和性质、角平分线的定义,中线的定义等知识,解题的关键是根据已知条件证明△AGC是等腰三角形,属于中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,是一副扑克牌中取出的两组牌,分别是红桃1,2,3和方块1,2,3,将它们的背面朝上分别重新洗牌后,再从两组牌中各摸出一张.
如图,是一副扑克牌中取出的两组牌,分别是红桃1,2,3和方块1,2,3,将它们的背面朝上分别重新洗牌后,再从两组牌中各摸出一张.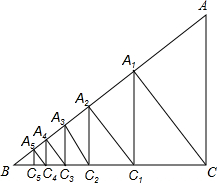 如图,已知直角△ACB,AC=3,BC=4,过直角顶点C作CA1⊥AB,垂足为A1,再过A1作A1C1⊥BC,垂足为C1;过C1作C1A2⊥AB,垂足为A2,再过A2作A2C2⊥BC,垂足为C2;…,这样一直做下去,得到一组线段A1C1,A2C2…,则线段AnCn为3×($\frac{4}{5}$)2n.(用含有n的代数式表示)
如图,已知直角△ACB,AC=3,BC=4,过直角顶点C作CA1⊥AB,垂足为A1,再过A1作A1C1⊥BC,垂足为C1;过C1作C1A2⊥AB,垂足为A2,再过A2作A2C2⊥BC,垂足为C2;…,这样一直做下去,得到一组线段A1C1,A2C2…,则线段AnCn为3×($\frac{4}{5}$)2n.(用含有n的代数式表示)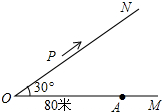 如图,∠MON=30°,在距离O点80米的A处有一所学校,当重型运输卡车P沿道路ON方向行驶时,距离卡车50米范围内都会受到卡车噪声的影响.
如图,∠MON=30°,在距离O点80米的A处有一所学校,当重型运输卡车P沿道路ON方向行驶时,距离卡车50米范围内都会受到卡车噪声的影响.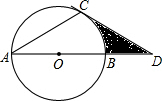 如图,⊙O的直径AB为12点D在AB的延长线上,DC切⊙O于点C,且∠DAC=30°,则图中阴影部分面积为18$\sqrt{3}$-6π.
如图,⊙O的直径AB为12点D在AB的延长线上,DC切⊙O于点C,且∠DAC=30°,则图中阴影部分面积为18$\sqrt{3}$-6π.