题目内容
19.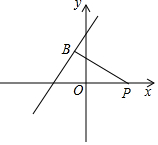 如图,点P的坐标为(2,0),点B在直线y=x+m上运动,当线段PB最短时,PB的长度是$\sqrt{2}$+$\frac{\sqrt{2}}{2}$m.
如图,点P的坐标为(2,0),点B在直线y=x+m上运动,当线段PB最短时,PB的长度是$\sqrt{2}$+$\frac{\sqrt{2}}{2}$m.
分析 当线段PB最短时,PB与直线y=x+m垂直,根据解析式即可求得C、D的坐标,然后根据勾股定理求得CD,然后根据三角形相似即可求得PB的最短长度.
解答 解:当线段PB最短时,PB⊥CD,如图所示:
由直线y=-x+m可知,直线与坐标轴的交点为C(-m,0),D(0,m),
∴OC=m,OD=m,
∴CD=$\sqrt{2}$m,
∵点P的坐标为(2,0),
∴PC=2+m,
∵∠PCB=∠DCO,∠PBC=∠DOC=90°,
∴△PBC∽△DOC,
∴$\frac{PB}{OD}=\frac{PC}{CD}$,即$\frac{PB}{m}=\frac{2+m}{\sqrt{2}m}$,
∴PB=$\sqrt{2}$+$\frac{\sqrt{2}}{2}$m.
故答案为:$\sqrt{2}$+$\frac{\sqrt{2}}{2}$m.
点评 本题考查了垂线段最短的性质,一次函数图象上点的坐标特征,勾股定理的应用,三角形相似的判定和性质,熟知垂线段最短是解题的关键.

练习册系列答案
 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
4.在△ABC中,点D,E分别在边AB,AC上,$\frac{AD}{BD}$=$\frac{1}{2}$,要使DE∥BC,还需满足下列条件中的( )
| A. | $\frac{DE}{BC}$=$\frac{1}{2}$ | B. | $\frac{DE}{BC}$=$\frac{1}{3}$ | C. | $\frac{AE}{AC}$=$\frac{1}{2}$ | D. | $\frac{AE}{AC}$=$\frac{1}{3}$ |
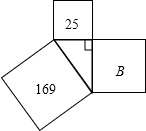 如图所示.以直角三角形的三条边为边长分别作正方形.依据图中所给条件,回答下列问题:
如图所示.以直角三角形的三条边为边长分别作正方形.依据图中所给条件,回答下列问题: