题目内容
4.已知关于a的方程$\frac{1}{2}$a+2=2(a-5)的解是关于x 的方程2(x-3)-b=-1的解2倍.(1)求a、b的值;
(2)若线段AB=a,在直线AB上取一点P,恰好使$\frac{AP}{BP}$=b,点E为PB的中点,求AE的长.
分析 (1)解一元一次方程求出a,根据题意求出x,根据方程的解的定义求出b;
(2)根据比例的性质求出AP,根据线段中点的概念求出PE,计算即可.
解答 解:(1)$\frac{1}{2}$a+2=2(a-5),
a+4=4a-20,
解得,a=8,
则x=4,
∴2(4-3)-b=-1,
解得,b=3;
(2)∵$\frac{AP}{BP}$=b,
∴$\frac{AP}{BP+AP}$=$\frac{b}{b+1}$,
∴AP=$\frac{ab}{b+1}$,
则BP=a-$\frac{ab}{b+1}$=$\frac{a}{b+1}$,
∵点E为PB的中点,
∴PE=$\frac{a}{2b+2}$,
∴AE=AP+PE=$\frac{2ab+a}{2b+2}$.
点评 本题考查的是一元一次方程的解法、两点间的距离的计算,掌握解一元一次方程的一般步骤、理解线段中点的概念是解题的关键.

练习册系列答案
相关题目
9. 如图所示几何体的主视图是( )
如图所示几何体的主视图是( )
 如图所示几何体的主视图是( )
如图所示几何体的主视图是( )| A. |  | B. |  | C. |  | D. |  |
16.在Rt△AABC中,∠C=90°,BC=3,AB=5,则sinA的值为( )
| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{4}$ |
13.有一组数据是5,2,3,6,4,则这组数据的方差是( )
| A. | 2 | B. | $\sqrt{2}$ | C. | 10 | D. | $\sqrt{10}$ |
14. 在灯塔O处观测到轮船P位于北偏西55°的方向,同时轮船Q在南偏东15°的方向,那么∠POQ的大小为( )
在灯塔O处观测到轮船P位于北偏西55°的方向,同时轮船Q在南偏东15°的方向,那么∠POQ的大小为( )
 在灯塔O处观测到轮船P位于北偏西55°的方向,同时轮船Q在南偏东15°的方向,那么∠POQ的大小为( )
在灯塔O处观测到轮船P位于北偏西55°的方向,同时轮船Q在南偏东15°的方向,那么∠POQ的大小为( )| A. | 160° | B. | 140° | C. | 110° | D. | 70° |
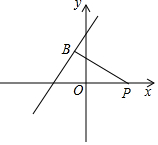 如图,点P的坐标为(2,0),点B在直线y=x+m上运动,当线段PB最短时,PB的长度是$\sqrt{2}$+$\frac{\sqrt{2}}{2}$m.
如图,点P的坐标为(2,0),点B在直线y=x+m上运动,当线段PB最短时,PB的长度是$\sqrt{2}$+$\frac{\sqrt{2}}{2}$m.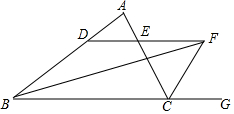 如图,∠ABC的平分线BF与△ABC中∠ACB的相邻外角∠ACG的平分线CF相交于点F,过F作DF∥BC,交AB于D,交AC于E,若BD=8cm,DE=3cm,求CE的长.
如图,∠ABC的平分线BF与△ABC中∠ACB的相邻外角∠ACG的平分线CF相交于点F,过F作DF∥BC,交AB于D,交AC于E,若BD=8cm,DE=3cm,求CE的长.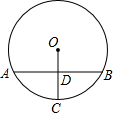 如图,⊙O的弦AB与半径OC垂直,点D为垂足,OD=DC,AB=2$\sqrt{3}$,点E在⊙O上,∠EOA=30°,则△EOC的面积为1或2.
如图,⊙O的弦AB与半径OC垂直,点D为垂足,OD=DC,AB=2$\sqrt{3}$,点E在⊙O上,∠EOA=30°,则△EOC的面积为1或2. 阅读下面材料:下面是“作角的平分线”的尺规作图过程.
阅读下面材料:下面是“作角的平分线”的尺规作图过程.