题目内容
3.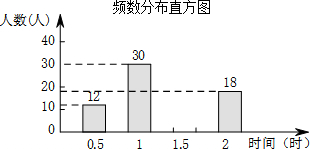 在某市开展的“美丽春城,创卫我同行”活动中,某校倡议七年级学生利用双休日在各自社区参加义务劳动.为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制成如下不完整的统计图表:
在某市开展的“美丽春城,创卫我同行”活动中,某校倡议七年级学生利用双休日在各自社区参加义务劳动.为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制成如下不完整的统计图表:某校七年级部分同学的劳动时间频数分布表
| 劳动时间(时) | 频数 |
| 0.5 | 12 |
| 1 | 30 |
| 1.5 | m |
| 2 | 18 |
| 合计 | 100 |
(2)被调查同学劳动时间的中位数是1.5小时.
(3)求被调查同学的平均劳动时间.
分析 (1)利用总人数减去其它组的人数求得m的值,进而补全直方图;
(2)根据中位数的定义求解;
(3)利用加权平均数公式即可求解.
解答 解:(1)m=100-12-30-18=40.
如图. ;
;
(2)同学劳动时间的中位数是1.5小时,故答案是:1.5;
(3)被调查同学的平均劳动时间为$\frac{1}{100}(0.5×12+1×30+1.5×40+2×18)=1.32$(小时).
点评 本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
相关题目
13.某市政府为了增强城镇居民抵御大病风险的能力,积极完善城镇居民医疗保险制度,纳入医疗保险的居民大病住院医疗费用的报销比例标准如下表:
设享受医保的某居民一年的大病住院医疗费用为x元,按上述标准报销的金额为y元.请写出800<x≤3000时,y关于x的函数关系式为y=$\frac{1}{2}$x-400.
| 医疗费用范围 | 报销比例标准 |
| 不超过800元 | 不予报销 |
| 超过800元且不超过3000元的部分 | 50% |
| 超过3000元且不超过5000元的部分 | 60% |
| 超过5000元的部分 | 70% |
14. 如图,在Rt△ABC中,∠B=90°,cosA=$\frac{12}{13}$,则tanA=( )
如图,在Rt△ABC中,∠B=90°,cosA=$\frac{12}{13}$,则tanA=( )
 如图,在Rt△ABC中,∠B=90°,cosA=$\frac{12}{13}$,则tanA=( )
如图,在Rt△ABC中,∠B=90°,cosA=$\frac{12}{13}$,则tanA=( )| A. | $\frac{12}{5}$ | B. | $\frac{13}{12}$ | C. | $\frac{12}{13}$ | D. | $\frac{5}{12}$ |
15.2016年5月4日,某校举行“我说我校训”演讲比赛,参赛选手共有12名.梦梦根据比赛中七位评委所给的某位参赛选手的分数制作了表格,如果去掉一个最高分和一个最低分,则表中数据一定不发生变化的是( )
| 众数 | 中位数 | 平均数 | 方差 |
| 9.2 | 9.1 | 9.1 | 0.2 |
| A. | 平均数 | B. | 众数 | C. | 中位数 | D. | 方差 |
13. 如图所示,△ABC≌△DEC,则不能得到的结论是( )
如图所示,△ABC≌△DEC,则不能得到的结论是( )
 如图所示,△ABC≌△DEC,则不能得到的结论是( )
如图所示,△ABC≌△DEC,则不能得到的结论是( )| A. | AB=DE | B. | ∠A=∠D | C. | BC=CD | D. | ∠ACD=∠BCE |
 在平面直角坐标系xOy中,抛物线y=ax2+bx+4经过A(-3,0)、B(4,0)两点,且与y轴交于点C,点D在x轴的负半轴上,且BD=BC,一动点P从点A出发,沿线段AB以每秒1个单位长度的速度向点B移动,同时另一个动点Q从点C出发,沿线段CA以某一速度向点A移动.
在平面直角坐标系xOy中,抛物线y=ax2+bx+4经过A(-3,0)、B(4,0)两点,且与y轴交于点C,点D在x轴的负半轴上,且BD=BC,一动点P从点A出发,沿线段AB以每秒1个单位长度的速度向点B移动,同时另一个动点Q从点C出发,沿线段CA以某一速度向点A移动.