题目内容
11.学校要培训一批校园记者成立编辑部创办校刊,九年级(1)班有2名学生和1名男生为候选人,每人被选中的可能性相同.(1)小明认为,如果从3名候选人中随机选拔1名,不是男生就是女生,因此选出的校园记者是男生和女生的可能性相等,你同意他的说法吗?为什么?
(2)如果每人最多只参加一次培训,从这个班的候选人中随机选拔两次,每次选拔1名参加培训,请用列表或画树状图的方法,求出参加第一次培训的是女生,参加第二次培训的是男生的概率.
分析 (1)利用概率公式分别计算出选中女生的概率和选中男生的概率,然后比较两个概率的大小即可判断选出的校园记者是男生和女生的可能性是否相等;
(2)画树状图展示所有6种等可能的结果数,再找出参加第一次培训的是女生,参加第二次培训的是男生的结果数,然后根据概率公式求解.
解答 解:(1)不同意他的说法.理由如下:
因为有2名女生和1名男生,每人被选中的可能性相等,
所以选中女生的概率=$\frac{2}{3}$,选中男生的概率=$\frac{1}{3}$,
而$\frac{2}{3}$>$\frac{1}{3}$,
所以选出的校园记者是男生和女生的可能性不相等;
(2)画树状图为:
共有6种等可能的结果数,其中参加第一次培训的是女生,参加第二次培训的是男生的结果数为2,
所以参加第一次培训的是女生,参加第二次培训的是男生的概率=$\frac{2}{6}$=$\frac{1}{3}$.
点评 本题考查了列表法与树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.也考查了可能性的大小.

练习册系列答案
相关题目
19.下列图案中,可以看作是中心对称图形的有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.计算(-2xy3)2的结果是( )
| A. | -4x2y6 | B. | 4x2y6 | C. | -4x2y9 | D. | 2x2y9 |
16. 某校男子足球队的年龄分布如下面的条形统计图,则这些队员年龄的众数和中位数分别是( )
某校男子足球队的年龄分布如下面的条形统计图,则这些队员年龄的众数和中位数分别是( )
 某校男子足球队的年龄分布如下面的条形统计图,则这些队员年龄的众数和中位数分别是( )
某校男子足球队的年龄分布如下面的条形统计图,则这些队员年龄的众数和中位数分别是( )| A. | $\frac{31}{2}$,15 | B. | 15,$\frac{31}{2}$ | C. | 15,15 | D. | $\frac{31}{2}$,$\frac{31}{2}$ |
3.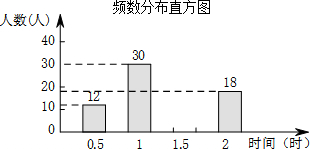 在某市开展的“美丽春城,创卫我同行”活动中,某校倡议七年级学生利用双休日在各自社区参加义务劳动.为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制成如下不完整的统计图表:
在某市开展的“美丽春城,创卫我同行”活动中,某校倡议七年级学生利用双休日在各自社区参加义务劳动.为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制成如下不完整的统计图表:
某校七年级部分同学的劳动时间频数分布表
(1)求m的值,并补全频数分布直方图.
(2)被调查同学劳动时间的中位数是1.5小时.
(3)求被调查同学的平均劳动时间.
 在某市开展的“美丽春城,创卫我同行”活动中,某校倡议七年级学生利用双休日在各自社区参加义务劳动.为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制成如下不完整的统计图表:
在某市开展的“美丽春城,创卫我同行”活动中,某校倡议七年级学生利用双休日在各自社区参加义务劳动.为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制成如下不完整的统计图表:某校七年级部分同学的劳动时间频数分布表
| 劳动时间(时) | 频数 |
| 0.5 | 12 |
| 1 | 30 |
| 1.5 | m |
| 2 | 18 |
| 合计 | 100 |
(2)被调查同学劳动时间的中位数是1.5小时.
(3)求被调查同学的平均劳动时间.
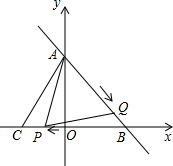 已知:如图,直线y=-$\frac{4}{3}$x+4与x轴、y轴分别相交于点A、B,点C的坐标是(-2,0).
已知:如图,直线y=-$\frac{4}{3}$x+4与x轴、y轴分别相交于点A、B,点C的坐标是(-2,0). 如图,在菱形ABCD中,E、F分别是AB和BC上的点,且BE=BF.
如图,在菱形ABCD中,E、F分别是AB和BC上的点,且BE=BF.