题目内容
14. 如图,在Rt△ABC中,∠B=90°,cosA=$\frac{12}{13}$,则tanA=( )
如图,在Rt△ABC中,∠B=90°,cosA=$\frac{12}{13}$,则tanA=( )| A. | $\frac{12}{5}$ | B. | $\frac{13}{12}$ | C. | $\frac{12}{13}$ | D. | $\frac{5}{12}$ |
分析 根据余弦,可得AC,BC的长,根据勾股定理,可得AB的长,根据正切函数的定义,可得答案.
解答 解:由Rt△ABC中,∠B=90°,cosA=$\frac{12}{13}$,得
AC=13a,AB=12a,
由勾股定理,得
BC=5a.
tanA=$\frac{BC}{AB}$=$\frac{5}{12}$,
故选:D.
点评 本题考查了锐角三角函数的定义,利用勾股定理得出AB的长是解题关键.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
19.下列图案中,可以看作是中心对称图形的有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.计算(-2xy3)2的结果是( )
| A. | -4x2y6 | B. | 4x2y6 | C. | -4x2y9 | D. | 2x2y9 |
3.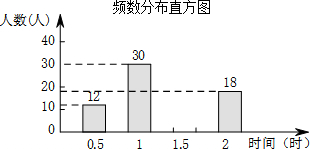 在某市开展的“美丽春城,创卫我同行”活动中,某校倡议七年级学生利用双休日在各自社区参加义务劳动.为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制成如下不完整的统计图表:
在某市开展的“美丽春城,创卫我同行”活动中,某校倡议七年级学生利用双休日在各自社区参加义务劳动.为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制成如下不完整的统计图表:
某校七年级部分同学的劳动时间频数分布表
(1)求m的值,并补全频数分布直方图.
(2)被调查同学劳动时间的中位数是1.5小时.
(3)求被调查同学的平均劳动时间.
 在某市开展的“美丽春城,创卫我同行”活动中,某校倡议七年级学生利用双休日在各自社区参加义务劳动.为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制成如下不完整的统计图表:
在某市开展的“美丽春城,创卫我同行”活动中,某校倡议七年级学生利用双休日在各自社区参加义务劳动.为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制成如下不完整的统计图表:某校七年级部分同学的劳动时间频数分布表
| 劳动时间(时) | 频数 |
| 0.5 | 12 |
| 1 | 30 |
| 1.5 | m |
| 2 | 18 |
| 合计 | 100 |
(2)被调查同学劳动时间的中位数是1.5小时.
(3)求被调查同学的平均劳动时间.
 已知:如图,直线y=-$\frac{4}{3}$x+4与x轴、y轴分别相交于点A、B,点C的坐标是(-2,0).
已知:如图,直线y=-$\frac{4}{3}$x+4与x轴、y轴分别相交于点A、B,点C的坐标是(-2,0). 如图所示,在完全重合放置的两张矩形纸片ABCD中,AB=4,BC=8,将上面的矩形纸片折叠,使点C与点A重合,折痕为EF,点D的对应点为G,连接DG,则图中阴影部分的面积为$\frac{18}{5}$.
如图所示,在完全重合放置的两张矩形纸片ABCD中,AB=4,BC=8,将上面的矩形纸片折叠,使点C与点A重合,折痕为EF,点D的对应点为G,连接DG,则图中阴影部分的面积为$\frac{18}{5}$.