题目内容
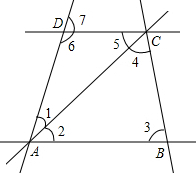
如图，在△ABC中，D是BC上一点，∠1=∠2，∠3=∠4，∠BAC=63°，求∠BAD的度数．考点：三角形内角和定理
专题：
分析：先根据三角形外角的性质得出∠3=∠1+∠2，再由∠1=∠2，∠3=∠4可得出∠4=∠1+∠2=2∠1，再根据三角形内角和定理求出∠2的度数即可．
解答：解：∵∠3是△ABD的外角，
∴∠3=∠1+∠2．
∵∠1=∠2，∠3=∠4，
∴∠4=∠1+∠2=2∠1，
∵∠2+∠4+∠BAC=180°，∠BAC=63°，
∴3∠1+63°=180°，
解得∠1=39°，即∠BAD=39°．
∴∠3=∠1+∠2．
∵∠1=∠2，∠3=∠4，
∴∠4=∠1+∠2=2∠1，
∵∠2+∠4+∠BAC=180°，∠BAC=63°，
∴3∠1+63°=180°，
解得∠1=39°，即∠BAD=39°．
点评：本题考查的是三角形内角和定理，熟知三角形内角和是180°是解答此题的关键．
练习册系列答案
相关题目
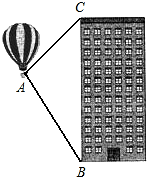桐城市某房产公司推出热气球观房活动，热气球的探测器显示，从热气球A处看某小区内一栋高楼顶部的仰角为30°，看这栋高楼底部的俯角为60°，A处于高楼的水平距离为30m，求这栋高楼有多高？（结果精确到1m，参考数据：
如图，△ABC内接于⊙O，AB过点O，若∠BAC=30°，则∠B的度数为（ ）| A、55° | B、60° |
| C、65° | D、70° |
如图所示，从标有数字的角中找出：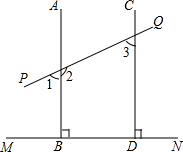
如图，直线AB、CD被直线PQ所截，且都垂直于MN，若∠3=3∠1-∠2，那么∠1=
在△ABC中，AB=9，AC=5，AD是∠BAC的平分线交BC于点D（如图），△ABD沿直线AD翻折后，点B落到点B1处，如果∠B1DC=