题目内容
观察下列等式:
=1-
•
=
-
•
=
-
,将以上三个等式两边分别相加,得
+
+
=1-
+
-
+
-
=1-
=
.
(1)猜想并写出:
= .
(2)直接写出下列各式的计算结果:
①
+
+
+…+
= ;
②
+
+
+…+
= .
| 1 |
| 1×2 |
| 1 |
| 2 |
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
(1)猜想并写出:
| 1 |
| n(n+1) |
(2)直接写出下列各式的计算结果:
①
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 2014×2015 |
②
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| n(n+1) |
考点:有理数的混合运算
专题:计算题
分析:(1)根据题意得出拆项规律,写出即可;
(2)利用拆项法把各式变形,计算即可得到结果.
(2)利用拆项法把各式变形,计算即可得到结果.
解答:解:(1)根据题意得:
=
-
;
(2)①原式=1-
+
-
+…+
-
=1-
=
;
②原式=1-
+
-
+…+
-
=1-
=
.
故答案为:(1)
-
;(2)①
;②
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
(2)①原式=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2014 |
| 1 |
| 2015 |
| 1 |
| 2015 |
| 2014 |
| 2015 |
②原式=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+1 |
| n |
| n+1 |
故答案为:(1)
| 1 |
| n |
| 1 |
| n+1 |
| 2014 |
| 2015 |
| n |
| n+1 |
点评:此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
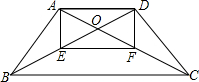 如图,在梯形ABCD中,AD∥BC,AB=CD,对角线AC与BD交于点O,E、F分别为OB、OC的中点.
如图,在梯形ABCD中,AD∥BC,AB=CD,对角线AC与BD交于点O,E、F分别为OB、OC的中点.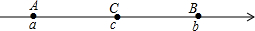 如图,已知数轴上点A、B、C所表示的数分别为a、b、c,点C是线段AB的中点,且AB=2,如果原点O的位置在线段AC上,那么|a+b-2c|等于( )
如图,已知数轴上点A、B、C所表示的数分别为a、b、c,点C是线段AB的中点,且AB=2,如果原点O的位置在线段AC上,那么|a+b-2c|等于( )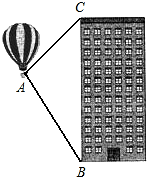 桐城市某房产公司推出热气球观房活动,热气球的探测器显示,从热气球A处看某小区内一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,A处于高楼的水平距离为30m,求这栋高楼有多高?(结果精确到1m,参考数据:
桐城市某房产公司推出热气球观房活动,热气球的探测器显示,从热气球A处看某小区内一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,A处于高楼的水平距离为30m,求这栋高楼有多高?(结果精确到1m,参考数据: