题目内容
1.一次函数y=-2x+3的图象与x轴的交点坐标为($\frac{3}{2}$,0).分析 令一次函数解析式中y=0,则可得出关于x的一元一次方程,解方程得出x值,从而得出一次函数图象与x轴的交点坐标.
解答 解:令y=-2x+3中y=0,则-2x+3=0,
解得:x=$\frac{3}{2}$.
∴一次函数y=-2x+3的图象与x轴的交点坐标为($\frac{3}{2}$,0).
故答案为:($\frac{3}{2}$,0).
点评 本题考查了一次函数图象上点的坐标特征,解题的关键是代入y=0得出-2x+3=0.本题属于基础题,难度不大,解决该题型题目时,令一次函数解析式中y(或x)=0,求出x(或y)值是关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
11.利用代入消元法解方程组$\left\{\begin{array}{l}{2x+3y=6①}\\{5x-3y=2②}\end{array}\right.$,下列做法正确的是( )
| A. | 由①得x=$\frac{6+3y}{2}$ | B. | 由①得y=$\frac{6-2x}{3}$ | C. | 由②得y=$\frac{-2+3x}{5}$ | D. | 由②得y=$\frac{5x+2}{3}$ |
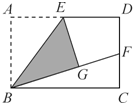 如图,在矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于点F.若CF=1,FD=2,则BC的长为2$\sqrt{6}$.
如图,在矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于点F.若CF=1,FD=2,则BC的长为2$\sqrt{6}$.