题目内容
10.如图(1),E为正方形ABCD的边AD上一点.AE:ED=1:$\sqrt{2}$,过E作EP⊥BD于P.连接AP、CP.BE与AP交于G.(1)证明:AP=CP;
(2)求∠ABE的度数;
(3)如图(2),点F在AD的延长线上,且PA=PF,PF交CD于H,连接CF,请写出线段AP与线段CF的数量关系,并说明理由.
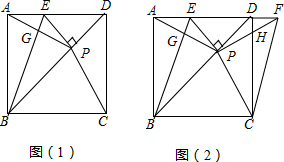
分析 (1)根据正方形的性质,判定△ADP≌△CDP,进而得到AP=CP;
(2)先根据△DEP是等腰直角三角形以及AE:ED=1:$\sqrt{2}$,得到AE=PE,再判定Rt△ABE≌Rt△PBE,最后求得∠ABE的度数;
(3)先根据等腰三角形的性质求得∠APC和∠APF的度数,进而计算出∠CPF为直角,得到△CPF为等腰直角三角形,根据其边角关系以及PA=PF=PC,得到线段AP与线段CF的数量关系.
解答  解:(1)∵正方形ABCD中,AD=CD=45°
解:(1)∵正方形ABCD中,AD=CD=45°
∴在△ADP和△CDP中
$\left\{\begin{array}{l}{AD=CD}\\{∠ADP=∠CDP}\\{PD=PD}\end{array}\right.$
∴△ADP≌△CDP(SAS)
∴AP=CP;
(2)∵EP⊥BD,∠EDP=45°
∴△DEP是等腰直角三角形
∴PE:ED=1:$\sqrt{2}$
又∵AE:ED=1:$\sqrt{2}$
∴AE=PE
在Rt△ABE和Rt△PBE中
$\left\{\begin{array}{l}{BE=BE}\\{AE=PE}\end{array}\right.$
∴Rt△ABE≌Rt△PBE(HL)
∴∠ABE=∠PBE=$\frac{1}{2}$∠ABD=22.5°
(3)线段AP与线段CF的数量关系为:CF=$\sqrt{2}$AP
由Rt△ABE≌Rt△PBE可得,AB=PB
∵∠ABP=45°
∴∠APB=67.5°=∠CPB,即∠APC=135°
∵AE=PE,∠PED=45°
∴∠PAE=22.5°
又∵PA=PF
∴∠APF=180°-2×22.5°=135°
∴∠CPF=360°-135°-135°=90°
又∵PA=PF=PC
∴△PCF是等腰直角三角形
∴CP:CF=1:$\sqrt{2}$
∴AP:CF=1:$\sqrt{2}$
即CF=$\sqrt{2}$AP
点评 本题主要考查了正方形的性质以及全等三角形的判定,解决问题的关键是根据等腰三角形的底角度数求得顶角度数,以及根据顶角度数求得底角度数.解题时注意,在等腰直角三角形中,其直角边与斜边的比值为1:$\sqrt{2}$,即底边长是腰长的$\sqrt{2}$倍.

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案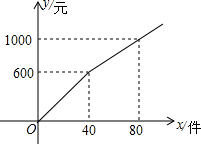 商户小李以每件6元的价格购进某商品若干件到市场去销售,销售金额y(元)与销售量x(件)的函数关系的图象如图所示,则降价后每件商品销售的价格为( )
商户小李以每件6元的价格购进某商品若干件到市场去销售,销售金额y(元)与销售量x(件)的函数关系的图象如图所示,则降价后每件商品销售的价格为( )| A. | 5元 | B. | 10元 | C. | 12.5元 | D. | 15元 |
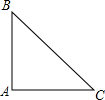 在△ABC中,∠BAC=90°,AB=AC=4,在△ABC的外部,以AB为直角边作等腰直角△ABD,连接CD,则△BCD的周长为4$\sqrt{5}$+4$\sqrt{2}$+4或8$\sqrt{2}$+8.
在△ABC中,∠BAC=90°,AB=AC=4,在△ABC的外部,以AB为直角边作等腰直角△ABD,连接CD,则△BCD的周长为4$\sqrt{5}$+4$\sqrt{2}$+4或8$\sqrt{2}$+8.
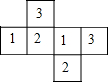 一个质地均匀的正方体的每个面上都标有数字1,2,3中的一个,其展开图如图所示,随机抛掷此正方体一次,则朝上与朝下的面上数字相同的概率是$\frac{1}{3}$.
一个质地均匀的正方体的每个面上都标有数字1,2,3中的一个,其展开图如图所示,随机抛掷此正方体一次,则朝上与朝下的面上数字相同的概率是$\frac{1}{3}$.