题目内容
11.利用代入消元法解方程组$\left\{\begin{array}{l}{2x+3y=6①}\\{5x-3y=2②}\end{array}\right.$,下列做法正确的是( )| A. | 由①得x=$\frac{6+3y}{2}$ | B. | 由①得y=$\frac{6-2x}{3}$ | C. | 由②得y=$\frac{-2+3x}{5}$ | D. | 由②得y=$\frac{5x+2}{3}$ |
分析 根据一元一次方程的解法分别表示出两个方程的x、y,然后选择即可.
解答 解:由①得,2x=6-3y,
x=$\frac{6-3y}{2}$;
3y=6-2x,
y=$\frac{6-2x}{3}$;
由②得,5x=2+3y,
x=$\frac{2+3y}{5}$,
3y=5x-2,
y=$\frac{5x-2}{3}$.
故选B.
点评 本题考查了解二元一次方程组,主要是代入消元法y=kx+b形式的转化,是基础题.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
2.滕州市出租车的收费标准是:起步价6元(即行驶距离不超过3千米都需付6元车费),超过3千米以后,每增加1千米,加收1.5元(不足1千米按1千米计).某人从甲地到乙地路程是x千米,出租车费为16.5元,那么x的最大值是( )
| A. | 11 | B. | 10 | C. | 9 | D. | 8 |
16.用加减法解方程组$\left\{\begin{array}{l}{2x+3y=3}\\{3x-2y=11}\end{array}\right.$时,下列四种变形中正确的是( )
| A. | $\left\{\begin{array}{l}{4x+6y=3}\\{9x-6y=11}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{6x+3y=9}\\{6x-2y=22}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{4x+6y=6}\\{9x-6y=33}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{6x+9y=3}\\{6x-4y=11}\end{array}\right.$ |
20.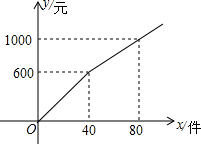 商户小李以每件6元的价格购进某商品若干件到市场去销售,销售金额y(元)与销售量x(件)的函数关系的图象如图所示,则降价后每件商品销售的价格为( )
商户小李以每件6元的价格购进某商品若干件到市场去销售,销售金额y(元)与销售量x(件)的函数关系的图象如图所示,则降价后每件商品销售的价格为( )
 商户小李以每件6元的价格购进某商品若干件到市场去销售,销售金额y(元)与销售量x(件)的函数关系的图象如图所示,则降价后每件商品销售的价格为( )
商户小李以每件6元的价格购进某商品若干件到市场去销售,销售金额y(元)与销售量x(件)的函数关系的图象如图所示,则降价后每件商品销售的价格为( )| A. | 5元 | B. | 10元 | C. | 12.5元 | D. | 15元 |