题目内容
6.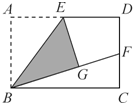 如图,在矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于点F.若CF=1,FD=2,则BC的长为2$\sqrt{6}$.
如图,在矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于点F.若CF=1,FD=2,则BC的长为2$\sqrt{6}$.
分析 首先过点E作EM⊥BC于M,交BF于N,易证得△ENG≌△BNM(AAS),MN是△BCF的中位线,根据全等三角形的性质,即可求得GN=MN,由折叠的性质,可得BG=3,继而求得BF的值,又由勾股定理,即可求得BC的长.
解答 解:过点E作EM⊥BC于M,交BF于N,
∵四边形ABCD是矩形,
∴∠A=∠ABC=90°,AD=BC,
∵∠EMB=90°,
∴四边形ABME是矩形,
∴AE=BM,
由折叠的性质得:AE=GE,∠EGN=∠A=90°,
∴EG=BM,
∵∠ENG=∠BNM,
∴△ENG≌△BNM(AAS),
∴NG=NM,
∴CM=DE,
∵E是AD的中点,
∴AE=ED=BM=CM,
∵EM∥CD,
∴BN:NF=BM:CM,
∴BN=NF,
∴NM=$\frac{1}{2}$CF=$\frac{1}{2}$,
∴NG=$\frac{1}{2}$,
∵BG=AB=CD=CF+DF=3,
∴BN=BG-NG=3-$\frac{1}{2}$=$\frac{5}{2}$,
∴BF=2BN=5,
∴BC=$\sqrt{B{F}^{2}-C{F}^{2}}$=$\sqrt{{5}^{2}-{1}^{2}}$=2$\sqrt{6}$,
故答案为:2$\sqrt{6}$.
点评 此题考查了矩形的判定与性质、折叠的性质、三角形中位线的性质以及全等三角形的判定与性质.此题难度适中,注意辅助线的作法,注意数形结合思想的应用.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
16.用加减法解方程组$\left\{\begin{array}{l}{2x+3y=3}\\{3x-2y=11}\end{array}\right.$时,下列四种变形中正确的是( )
| A. | $\left\{\begin{array}{l}{4x+6y=3}\\{9x-6y=11}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{6x+3y=9}\\{6x-2y=22}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{4x+6y=6}\\{9x-6y=33}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{6x+9y=3}\\{6x-4y=11}\end{array}\right.$ |
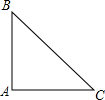 在△ABC中,∠BAC=90°,AB=AC=4,在△ABC的外部,以AB为直角边作等腰直角△ABD,连接CD,则△BCD的周长为4$\sqrt{5}$+4$\sqrt{2}$+4或8$\sqrt{2}$+8.
在△ABC中,∠BAC=90°,AB=AC=4,在△ABC的外部,以AB为直角边作等腰直角△ABD,连接CD,则△BCD的周长为4$\sqrt{5}$+4$\sqrt{2}$+4或8$\sqrt{2}$+8.