题目内容
15.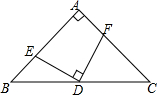 如图,在△ABC中,AB=AC,∠BAC=90°,D是BC中点,ED⊥FD,ED与AB交于E,FD与AC交于F.若BE=4cm,CF=6cm,则S△ABC=50cm2.
如图,在△ABC中,AB=AC,∠BAC=90°,D是BC中点,ED⊥FD,ED与AB交于E,FD与AC交于F.若BE=4cm,CF=6cm,则S△ABC=50cm2.
分析 连接AD,根据等腰直角三角形的性质,可得出AD=BD=CD,AD⊥BC,∠B=∠C=∠DAC=45°,从而可证得△BDE≌△ADF,推出BE=AF=4,求出AB、AC即可解决问题.
解答 证明:如图,连接AD,
∵AB=AC,∠BAC=90°,D是BC的中点,
∴AD=BD=CD,AD⊥BC,∠B=∠C=∠DAC=45°,
∵ED⊥FD,
∴∠BDE=∠ADF,
在△BDE和△ADF中,
$\left\{\begin{array}{l}{∠EBD=∠FAD}\\{∠EDB=∠FDA}\\{BD=AD}\end{array}\right.$,
∴△BDE≌△ADF(ASA),
∴BE=AF=4cm,∵CF=6cm,
∴AB=AC=10,
∴S△ABC=$\frac{1}{2}$×10×10=50(cm2),
故答案为50cm2.
点评 本题主要考查了等腰直角三角形的性质、全等三角形的判定与性质,难度适中.“三线合一”是等腰三角形常用辅助线,要熟练掌握.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.△ABC的三边长分别为a,b,c,下列条件:①∠A=∠B-∠C;②a2=(b+c)(b-c);③a:b:c=5:12:13.其中能判断△ABC是直角三角形的个数有( )
| A. | 0个 | B. | 1 个 | C. | 2个 | D. | 3个 |
7.下列说法正确的是( )
| A. | 百分数都小于1 | |
| B. | 圆的周长是这个圆的半径的3.14倍 | |
| C. | 在含糖7%的糖水中,糖和水的比是7:100 | |
| D. | 如果两个扇形的圆心角相相等,那么半径越长所对的弧长也越长 |
4.对于非零的实数a,b,规定a?b=$\frac{1}{b}$$-\frac{1}{a}$,若2?(2x-1)=1,则x=( )
| A. | $\frac{3}{2}$ | B. | $\frac{5}{4}$ | C. | $\frac{5}{6}$ | D. | $-\frac{1}{6}$ |
5.点A(x1,y1)、B(x2,y2)在函数y=$\frac{6}{x}$的图象上,若0<x2<x1,则y1、y2的大小关系是( )
| A. | y2<y1 | B. | y1=y2 | ||
| C. | y1<y2 | D. | y1、y2的大小关系不确定 |
 如图,在△ABC中,∠C=90°,AE平分∠A交BC于E,CD⊥AB于D,交AE于F,FM∥AB交BC于M,求证(1)$\frac{AE}{AF}=\frac{AB}{AC}$;(2)$\frac{EB}{MB}=\frac{AE}{AF}$;(3)CE=BM.
如图,在△ABC中,∠C=90°,AE平分∠A交BC于E,CD⊥AB于D,交AE于F,FM∥AB交BC于M,求证(1)$\frac{AE}{AF}=\frac{AB}{AC}$;(2)$\frac{EB}{MB}=\frac{AE}{AF}$;(3)CE=BM.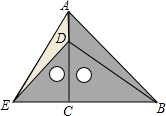 把等腰直角三角板ABC和等腰直角三角板ECD如图放置,点D在AC上,连接AE、BD,试判断AE与BD的关系,并说明理由.
把等腰直角三角板ABC和等腰直角三角板ECD如图放置,点D在AC上,连接AE、BD,试判断AE与BD的关系,并说明理由. 如图,图中共有6 条线段,7 个小于平角的角.
如图,图中共有6 条线段,7 个小于平角的角.