题目内容
2.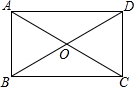 如图,在四边形ABCD中,点O是AC的中点,
如图,在四边形ABCD中,点O是AC的中点,(1)若AB∥CD,求证:△OAB≌△OCD;
(2)在问题(1)中,若AC=BD,则四边形ABCD是矩形.
分析 (1)由ASA证得这两个三角形全等;
(2)利用(1)中全等三角形的性质判定AB=CD,则四边形ABCD是平行四边形,则根据”对角线相等的平行四边形为矩形“推知四边形ABCD是矩形.
解答  (1)证明:如图,∵在四边形ABCD中,点O是AC的中点,
(1)证明:如图,∵在四边形ABCD中,点O是AC的中点,
∴OA=OC.
又∵AB∥CD,
∴∠OAB=∠OCD,
在△OAB与△OCD中,
$\left\{\begin{array}{l}{∠OAB=∠OCD}\\{OA=OC}\\{∠AOB=∠COD}\end{array}\right.$,
∴△OAB≌△OCD(ASA);
(2)由(1)知,△OAB≌△OCD,则AB=CD.
又∵AB∥CD,
∴四边形ABCD是平行四边形,
又∵AC=BD,
∴平行四边形ABCD是矩形.
故答案是:矩形.
点评 本题考查了全等三角形的判定与性质、矩形的判定.在应用全等三角形的判定时,要注意三角形间的公共边、公共角以及对顶角,必要时添加适当辅助线构造三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.二次根式$\sqrt{1-x}$中,x的取值范围是( )
| A. | x>1 | B. | x≥1 | C. | x<1 | D. | x≤1 |
14. 如图,AD∥BC,∠B=30°,DB平分∠ADE,则∠DEC的度数为( )
如图,AD∥BC,∠B=30°,DB平分∠ADE,则∠DEC的度数为( )
 如图,AD∥BC,∠B=30°,DB平分∠ADE,则∠DEC的度数为( )
如图,AD∥BC,∠B=30°,DB平分∠ADE,则∠DEC的度数为( )| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
12.下面的几何体中,俯视图为三角形的是( )
| A. |  | B. |  | C. |  | D. |  |
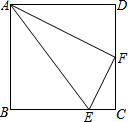 如图,E、F分别是正方形ABCD中BC和CD边上的点,CE=$\frac{1}{4}$BC,F为CD的中点,连接AF、AE、EF,
如图,E、F分别是正方形ABCD中BC和CD边上的点,CE=$\frac{1}{4}$BC,F为CD的中点,连接AF、AE、EF,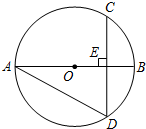 如图,已知在⊙O中,弦CD垂直于直径AB,垂足为点E,如果∠BAD=30°,OE=2,那么CD=4$\sqrt{3}$.
如图,已知在⊙O中,弦CD垂直于直径AB,垂足为点E,如果∠BAD=30°,OE=2,那么CD=4$\sqrt{3}$.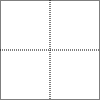 如图是由4个边长为1的正方形构成的田字格,只用没有刻度的直尺在这个田字格中最多可以作出8条长度为$\sqrt{5}$的线段.
如图是由4个边长为1的正方形构成的田字格,只用没有刻度的直尺在这个田字格中最多可以作出8条长度为$\sqrt{5}$的线段.