题目内容
12.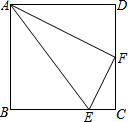 如图,E、F分别是正方形ABCD中BC和CD边上的点,CE=$\frac{1}{4}$BC,F为CD的中点,连接AF、AE、EF,
如图,E、F分别是正方形ABCD中BC和CD边上的点,CE=$\frac{1}{4}$BC,F为CD的中点,连接AF、AE、EF,(1)判定△AEF的形状,并说明理由;
(2)设AE的中点为O,判定∠BOF和∠BAF的数量关系,并证明你的结论.
分析 (1)正方形的边长相等,因为设AB=4a,所以其他三边也为4a,正方形的四个角都是直角,所以能求出AE,AF,EF的长,从而可判断出三角形的形状;
(2)根据直角三角形斜边中线的性质解答即可.
解答 解:设AB=4a,
∵AB=4a,CE=$\frac{1}{4}$BC,
∴EC=a,BE=3a,
∵F为CD的中点,
∴DF=FC=2a,
∴EF=$\sqrt{(2{a)}^{2}+(a)^{2}}=\sqrt{5}a$,
AF=$\sqrt{(4a)^{2}+(2a)^{2}}=\sqrt{20}a$,
AE=$\sqrt{(4a)^{2}+(3a)^{2}}=5a$.
∴AE2=EF2+AF2.
∴△AEF是直角三角形;
(2)∠BOF=2∠BAF,理由如下: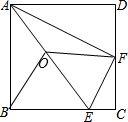
∵AE的中点为O,
∵△ABE是直角三角形,△AFE是直角三角形,
∴AO=OB=OE,OE=OA=OF,
∴∠BAO=∠OAB,∠OAF=∠OFA,
∴∠BOF=∠BAO+∠OAB+∠OAF+∠OFA=2∠BAF.
点评 本题考查了正方形的性质,四个边相等,四个角相等,勾股定理以及勾股定理的逆定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.已知$\sqrt{a-2}$+|b+3|=0,则P(-a,-b)的坐标为( )
| A. | (2,3) | B. | (2,-3) | C. | (-2,3) | D. | (-2,-3) |

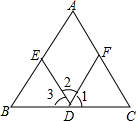 如图,(1)因为∠A=∠BED(已知),
如图,(1)因为∠A=∠BED(已知),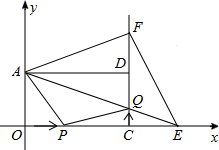 如图,在平面直角坐标系xOy中,矩形AOCD的顶点A的坐标是(0,4),现有两动点P,Q,点P从点O出发沿线段OC(不包括端点O,C)以每秒2个单位长度的速度匀速向点C运动,点Q从点C出发沿线段CD(不包括端点C,D)以每秒1个单位长度的速度匀速向点D运动.点P,Q同时出发,同时停止,设运动时间为t(秒),当t=2(秒)时,PQ=2$\sqrt{5}$.
如图,在平面直角坐标系xOy中,矩形AOCD的顶点A的坐标是(0,4),现有两动点P,Q,点P从点O出发沿线段OC(不包括端点O,C)以每秒2个单位长度的速度匀速向点C运动,点Q从点C出发沿线段CD(不包括端点C,D)以每秒1个单位长度的速度匀速向点D运动.点P,Q同时出发,同时停止,设运动时间为t(秒),当t=2(秒)时,PQ=2$\sqrt{5}$. 如图,在四边形ABCD中,点O是AC的中点,
如图,在四边形ABCD中,点O是AC的中点,