题目内容
13．
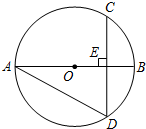如图，已知在⊙O中，弦CD垂直于直径AB，垂足为点E，如果∠BAD=30°，OE=2，那么CD=4$\sqrt{3}$．
分析 连接OD，弦CD垂直于直径AB，∠BAD=30°，由圆周角定理得∠BOD=60°，设半径为r，则OE=$\frac{1}{2}r$，r=4，得DE，CD．
解答 解：连接OD，
∵∠BAD=30°，
∴∠BOD=60°，
设半径为r，
OE=$\frac{1}{2}$r，OE=2，
∴r=4，
∴DE=$\frac{\sqrt{3}}{2}$×4=2$\sqrt{3}$，
∴$CD=4\sqrt{3}$．
故答案为：4$\sqrt{3}$．
点评 本题主要考查了垂径定理，圆周角定理，特殊角的三角函数，熟练运用特殊角的三角函数是解答此题的关键．
练习册系列答案
相关题目
1．已知$\sqrt{a-2}$+|b+3|=0，则P（-a，-b）的坐标为（ ）
| A． | （2，3） | B． | （2，-3） | C． | （-2，3） | D． | （-2，-3） |
8．若点A在第二象限，且到x轴的距离为2，到y轴的距离为3，则点A的坐标为（ ）
| A． | （-3，2） | B． | （3，-2） | C． | （-2，3） | D． | （2，-3） |
18．下列运算错误的是（ ）
| A． | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B． | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ | C． | $\sqrt{8}$+$\sqrt{2}$=2 | D． | （-$\sqrt{3}$）2=3 |
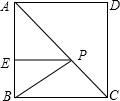如图，正方形ABCD中，点E在边AB上，且BE=$\sqrt{2}$，AE=3BE，点P在线段AC上的运动，则PE+PB的最小值为5$\sqrt{2}$．
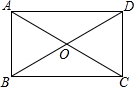如图，在四边形ABCD中，点O是AC的中点，