题目内容
 如图,在平面直角坐标系中,抛物线y=ax2+3与y轴交于点A,过点与x轴平行的直线交抛物线y=
如图,在平面直角坐标系中,抛物线y=ax2+3与y轴交于点A,过点与x轴平行的直线交抛物线y=| 1 |
| 3 |
考点:二次函数的性质
专题:计算题
分析:先根据y轴上点的坐标特征得到A点的坐标为(0,3),再利用BC∥x轴得到B点、C点的纵坐标都为3,然后对于函数y=
x2于点B,计算出函数值为3所对应的自变量即可得到B、C点的坐标,再计算BC的长度.
| 1 |
| 3 |
解答:解:当x=0时,y=ax2+3=3,则A点坐标为(0,3),
因为BC∥x轴,
所以B点、C点的纵坐标都为3,
当y=3时,
x2=3,解得x1=-3,x2=-3,
所以B点坐标为(-3,0),C点坐标为(3,0),
所以BC=3-(-3)=6.
因为BC∥x轴,
所以B点、C点的纵坐标都为3,
当y=3时,
| 1 |
| 3 |
所以B点坐标为(-3,0),C点坐标为(3,0),
所以BC=3-(-3)=6.
点评:本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-
,
),对称轴直线x=-
,二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<-
时,y随x的增大而减小;x>-
时,y随x的增大而增大;x=-
时,y取得最小值
,即顶点是抛物线的最低点.当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-
时,y随x的增大而增大;x>-
时,y随x的增大而减小;x=-
时,y取得最大值
,即顶点是抛物线的最高点.
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
 如图,已知正方形ABCD中,E是BC的中点,F是CD上一点,且FD=3CF,试判断△AEF的形状,并说明理由.
如图,已知正方形ABCD中,E是BC的中点,F是CD上一点,且FD=3CF,试判断△AEF的形状,并说明理由.
 如图,△ABT是等腰直角三角形,AB是⊙O的直径,且AB=4,则图中阴影部分的面积是
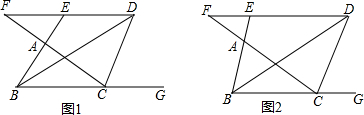
如图,△ABT是等腰直角三角形,AB是⊙O的直径,且AB=4,则图中阴影部分的面积是 如图所示,要使一个六边形木架在同一平面内不变形,至少还要再钉上几根木条?要使一个n边形(n≥4)木架在同一平面内不变形,至少还要再钉上几根木条?
如图所示,要使一个六边形木架在同一平面内不变形,至少还要再钉上几根木条?要使一个n边形(n≥4)木架在同一平面内不变形,至少还要再钉上几根木条?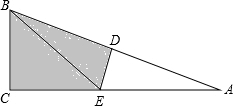 如图,在Rt△ABC中,∠C=90°,△ABC沿DE折叠,使得点A落在点B处,已知AC=6,BC=2,则四边形BCED的面积为
如图,在Rt△ABC中,∠C=90°,△ABC沿DE折叠,使得点A落在点B处,已知AC=6,BC=2,则四边形BCED的面积为 如图,在四边形ABCD中,∠A+∠C=180°,∠B=100°,∠ADE是四边形ABCD的一个外角,则∠ADE=
如图,在四边形ABCD中,∠A+∠C=180°,∠B=100°,∠ADE是四边形ABCD的一个外角,则∠ADE=