题目内容
已知点I为△ABC的内心，点O为△ABC的外心．若∠BOC=100°，则∠BIC= ．
考点：三角形的内切圆与内心,三角形的外接圆与外心
专题：
分析：利用三角形外心的性质得出∠A的度数，再利用三角形内角和定理以及三角形内心的性质得出答案．
解答：
解：∵点O为△ABC的外心，∠BOC=100°，
∴∠A=50°，
∵点I为△ABC的内心，
∴∠ABC+∠ACB=130°，则∠OBC+∠OCB=65°，
∴∠BIC=115°．
故答案为：115°．
解：∵点O为△ABC的外心，∠BOC=100°，∴∠A=50°，
∵点I为△ABC的内心，
∴∠ABC+∠ACB=130°，则∠OBC+∠OCB=65°，
∴∠BIC=115°．
故答案为：115°．
点评：此题主要考查了三角形的内心与外心，正确得出∠A的度数是解题关键．
练习册系列答案
相关题目
如图，己知∠1=145°，∠2=145°，则AB∥CD，依据是
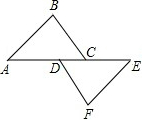如图，点A、D、C、E在同一条直线上，AB∥EF，AB=EF，∠B=∠F，AE=10，AC=7，则CD的长为（ ）| A、5.5 | B、4 | C、4.5 | D、3 |
如图矩形ABCD中，AB=6，BC=8，若将矩形折叠，使B点与D点重合，求折痕EF的长．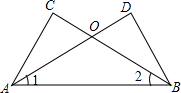
已知：如图，∠1=∠2，∠C=∠D．求证：
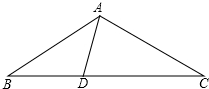在△ABC中，AB=AC=6，∠BAC=108°，点D在边BC上，∠BAD=36°．
如图，在平面直角坐标系中，抛物线y=ax2+3与y轴交于点A，过点与x轴平行的直线交抛物线y=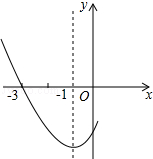
如图是二次函数y=ax2+bx+c图象的一部分，其对称轴是x=-1，且过点（-3，0），下列说法：①abc＜0；②2a-b=0；③4a+2b+c＜0；④若（-5，y1），（3，y2）是抛物线上两点，则y1＜y2，其中说法正确的是（ ）