题目内容
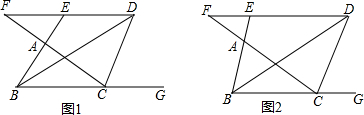
已知,如图(1)所示,△ABC的∠ABC的平分线BD与∠ACB的外角平分线交于D点,
(1)DE∥BC交BA的延长线于E,交CA延长线于F,求证:CF=EF+BE;
(2)如图(2),在(1)的条件下,∠ACB=30°,∠ABC=90°,DE=2,求△FCD的面积.
(1)DE∥BC交BA的延长线于E,交CA延长线于F,求证:CF=EF+BE;
(2)如图(2),在(1)的条件下,∠ACB=30°,∠ABC=90°,DE=2,求△FCD的面积.

考点:全等三角形的判定与性质
专题:
分析:(1)先根据角平分线的性质得出∠1=∠2,∠DCF=∠DCG,再由平行线的性质可知∠2=∠3,∠DCG=∠FDC,故可得出DE=BE,DF=CF,由此可得出结论;
(2)过点C作CH⊥BD于点H,由(1)知BE=DE,BC∥DE,再根据∠ABC=90°可知∠BED=90°,由勾股定理求出BD的长,再根据∠ACB=30°,CD是∠ACG的平分线可得出∠ACD的度数,由三角形内角和定理求出∠CDH的度数.设BH=CH=x,则DH=BD-x,根据锐角三角函数的定义得出x的值,进而可得出EF的值,由三角形的面积公式即可得出结论.
(2)过点C作CH⊥BD于点H,由(1)知BE=DE,BC∥DE,再根据∠ABC=90°可知∠BED=90°,由勾股定理求出BD的长,再根据∠ACB=30°,CD是∠ACG的平分线可得出∠ACD的度数,由三角形内角和定理求出∠CDH的度数.设BH=CH=x,则DH=BD-x,根据锐角三角函数的定义得出x的值,进而可得出EF的值,由三角形的面积公式即可得出结论.
解答: (1)证明:如图1所示,
(1)证明:如图1所示,
∵△ABC的∠ABC的平分线BD与∠ACB的外角平分线交于D点,
∵∠1=∠2,∠DCF=∠DCG.
∵DE∥BC,
∴∠2=∠3,∠DCG=∠FDC,
∴∠1=∠3,∠DCF=∠FDC,
∴DE=BE,DF=CF,
∴EF+DE=EF+BE=DF=CF,即CF=EF+BE;

(2)解:如图2,过点C作CH⊥BD于点H,由(1)知BE=DE,BC∥DE,
∵∠ABC=90°,BD平分角ABC,
∴∠BED=90°,∠DBC=45°.
∵DE=2,
∴BD=
=
=2
.
∵∠ACB=30°,
∴∠ACG=180°-30°=150°.
∵CD是∠ACG的平分线,
∴∠ACD=∠DCG=
×150°=75°,
∴∠EDC=∠DCG=75°,
∴∠CDH=∠EDC-∠EDB=75°-45°=30°.
设BH=CH=x,则DH=BD-x=2
-x,
∴
=tan∠CDH,即
=
,解得x=
-
,
∴BC=
=
=2
-2,
∴AB=BC•tan∠ACB=(2
-2)•
=2-
,
∴AE=BE-AB=2-2+
=
.
∵DE∥BC,
∴∠F=∠ABC=30°,
∴EF=
=
=2,
∴S△FCD=
(EF+DE)•BE=
×(2+2)×2=4.
 (1)证明:如图1所示,
(1)证明:如图1所示,∵△ABC的∠ABC的平分线BD与∠ACB的外角平分线交于D点,
∵∠1=∠2,∠DCF=∠DCG.
∵DE∥BC,
∴∠2=∠3,∠DCG=∠FDC,
∴∠1=∠3,∠DCF=∠FDC,
∴DE=BE,DF=CF,
∴EF+DE=EF+BE=DF=CF,即CF=EF+BE;

(2)解:如图2,过点C作CH⊥BD于点H,由(1)知BE=DE,BC∥DE,
∵∠ABC=90°,BD平分角ABC,
∴∠BED=90°,∠DBC=45°.
∵DE=2,
∴BD=
| DE2+BE2 |
| 22+22 |
| 2 |
∵∠ACB=30°,
∴∠ACG=180°-30°=150°.
∵CD是∠ACG的平分线,
∴∠ACD=∠DCG=
| 1 |
| 2 |
∴∠EDC=∠DCG=75°,
∴∠CDH=∠EDC-∠EDB=75°-45°=30°.
设BH=CH=x,则DH=BD-x=2
| 2 |
∴
| CH |
| DH |
| x | ||
2
|
| ||
| 3 |
| 6 |
| 2 |
∴BC=
| CH |
| sin∠DBC |
| ||||
|
| 3 |
∴AB=BC•tan∠ACB=(2
| 3 |
| ||
| 3 |
2
| ||
| 3 |
∴AE=BE-AB=2-2+
2
| ||
| 3 |
2
| ||
| 3 |
∵DE∥BC,
∴∠F=∠ABC=30°,
∴EF=
| AE |
| tan30° |
| ||||
|
∴S△FCD=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查的是解直角三角形的应用,涉及到角平分线的性质、等腰三角形的判定与性质、直角三角形的性质等知识,难度较大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
将数8200000用科学记数法表示为( )
| A、8.2×107 |
| B、82×105 |
| C、8.2×106 |
| D、0.82×107 |
现在网购越来越多地成为人们的一种消费方式,刚刚过去的2014年的“双11”网上促销活动中,天猫和淘宝的支付交易额突破571亿元,将571亿元用科学记数法表示为( )
| A、5.71×108 |
| B、5.71×1010 |
| C、5.71×109 |
| D、0.571×1011 |
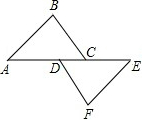 如图,点A、D、C、E在同一条直线上,AB∥EF,AB=EF,∠B=∠F,AE=10,AC=7,则CD的长为( )
如图,点A、D、C、E在同一条直线上,AB∥EF,AB=EF,∠B=∠F,AE=10,AC=7,则CD的长为( )| A、5.5 | B、4 | C、4.5 | D、3 |
 如图,已知△ABC中,BD平分∠ABC,点M是线段BD上一点,过M点作EF∥BC,分别交边AB、AC于点E、F,作MN∥AB交BC于点N.
如图,已知△ABC中,BD平分∠ABC,点M是线段BD上一点,过M点作EF∥BC,分别交边AB、AC于点E、F,作MN∥AB交BC于点N. 如图,己知∠1=145°,∠2=145°,则AB∥CD,依据是
如图,己知∠1=145°,∠2=145°,则AB∥CD,依据是
 如图矩形ABCD中,AB=6,BC=8,若将矩形折叠,使B点与D点重合,求折痕EF的长.
如图矩形ABCD中,AB=6,BC=8,若将矩形折叠,使B点与D点重合,求折痕EF的长. 如图,在平面直角坐标系中,抛物线y=ax2+3与y轴交于点A,过点与x轴平行的直线交抛物线y=
如图,在平面直角坐标系中,抛物线y=ax2+3与y轴交于点A,过点与x轴平行的直线交抛物线y=