题目内容
 如图,△ABT是等腰直角三角形,AB是⊙O的直径,且AB=4,则图中阴影部分的面积是
如图,△ABT是等腰直角三角形,AB是⊙O的直径,且AB=4,则图中阴影部分的面积是考点:扇形面积的计算
专题:
分析:连接OC,得出△BOC是直角三角形,∠AOC=90°,分别求出△ABT、△BOC和扇形OAC的面积,即可求出阴影部分的面积.
解答:解:如图所示: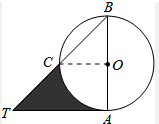 连接OC;
连接OC;
∵△ABT是等腰直角三角形,
∴∠BAT=90°,∠B=45°,AT=AB=4,
∵OC=OB=
AB=2,
∴∠BCO=∠B=45°,
∴∠BOC=90°,
∴∠AOC=90°,
∵S△ABT=
AB•AT=
×4×4=8,S扇形OAC=
π•22=π,S△BOC=
OB•OC=
×2×2=2,
∴S阴影=S△ABT-S△BOC-S扇形=8-2-π=6-π.
故答案为:6-π.
 连接OC;
连接OC;∵△ABT是等腰直角三角形,
∴∠BAT=90°,∠B=45°,AT=AB=4,
∵OC=OB=
| 1 |
| 2 |
∴∠BCO=∠B=45°,
∴∠BOC=90°,
∴∠AOC=90°,
∵S△ABT=
| 1 |
| 2 |
| 1 |
| 2 |
| 90 |
| 360 |
| 1 |
| 2 |
| 1 |
| 2 |
∴S阴影=S△ABT-S△BOC-S扇形=8-2-π=6-π.
故答案为:6-π.
点评:本题考查了直角三角形的面积和扇形面积的计算方法;弄清阴影部分的面积等于大三角形的面积减去小三角形和扇形的面积是关键.

练习册系列答案
相关题目

 如图所示,直线AE上有一点O,∠AOB=30°,∠BOC=2∠AOB
如图所示,直线AE上有一点O,∠AOB=30°,∠BOC=2∠AOB 如图,在平面直角坐标系中,抛物线y=ax2+3与y轴交于点A,过点与x轴平行的直线交抛物线y=
如图,在平面直角坐标系中,抛物线y=ax2+3与y轴交于点A,过点与x轴平行的直线交抛物线y= 如图,菱形ABCD的对角线AC与BD相交于点O,点E,F分别为边AB,AD的中点,连接EF,OE,OF,
如图,菱形ABCD的对角线AC与BD相交于点O,点E,F分别为边AB,AD的中点,连接EF,OE,OF, 如图,∠B的内错角,同旁内角各有哪些?请分别写出来.
如图,∠B的内错角,同旁内角各有哪些?请分别写出来.