题目内容
如图，在四边形ABCD中，∠A+∠C=180°，∠B=100°，∠ADE是四边形ABCD的一个外角，则∠ADE=考点：多边形内角与外角
专题：
分析：先根据四边形内角和为360°得出∠B+∠ADC=180°，再由邻补角定义得出∠ADE+∠ADC=180°，然后根据同角的补角相等即可得到∠ADE=∠B=100°．
解答：解：∵∠A+∠B+∠C+∠ADC=360°，∠A+∠C=180°，
∴∠B+∠ADC=360°-（∠A+∠C）=180°，
∵∠ADE+∠ADC=180°，
∴∠ADE=∠B=100°．
故答案为100°．
∴∠B+∠ADC=360°-（∠A+∠C）=180°，
∵∠ADE+∠ADC=180°，
∴∠ADE=∠B=100°．
故答案为100°．
点评：本题考查了多边形内角与外角，四边形内角和定理，补角的性质，比较简单．
练习册系列答案
优学名师名题系列答案
相关题目
如图，在平面直角坐标系中，抛物线y=ax2+3与y轴交于点A，过点与x轴平行的直线交抛物线y=
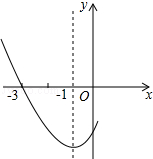如图是二次函数y=ax2+bx+c图象的一部分，其对称轴是x=-1，且过点（-3，0），下列说法：①abc＜0；②2a-b=0；③4a+2b+c＜0；④若（-5，y1），（3，y2）是抛物线上两点，则y1＜y2，其中说法正确的是（ ）| A、①② | B、②③ |
| C、①②④ | D、②③④ |
有理数a，b，c在数轴上对应的点如图所示，则下列式子中正确的是（ ）| A、a＞b |
| B、|a-c|=a-c |
| C、-a＜-b＜c |
| D、|b+c|=b+c |
如图，作出△ABC绕点C逆时针旋转60°的图形．
如图，∠B的内错角，同旁内角各有哪些？请分别写出来．
如图，在矩形ABCD中，E，F是BC上的两点，且BE=CF，连接AF，FD，相交于点P．求证：PA=PD．
如图，直角三角形DEF是由直角三角形ABC沿BC向右平移3cm得到的，如果AB=6cm，DH=2cm，求图中阴影部分的面积．已知x=2是2x+a=5的解，则a的值为（ ）
| A、1 | ||
B、
| ||
| C、-1 | ||
D、
|