题目内容
6.二次函数S=-t2+12t-20(0≤t≤10)的最大值是16,最小值是-20.分析 先求出二次函数的对称轴为直线x=6,然后根据二次函数的增减性解答即可.
解答 解:∵抛物线的对称轴为x=-$\frac{b}{2a}$=6,
∵a=-1<0,
∴x<6时,y随x的增大而增大,x>6时,y随x的增大而减小,
∴在0≤t≤10内,x=6时,y有最大值,x=0时y有最小值,分别是y=-36+72-20=16和y=-20,
故答案为:16,-20.
点评 本题考查了二次函数的最值问题,二次函数的增减性,根据函数解析式求出对称轴解析式是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18. 如图,图中对顶角共有( )对.
如图,图中对顶角共有( )对.
 如图,图中对顶角共有( )对.
如图,图中对顶角共有( )对.| A. | 3 | B. | 6 | C. | 8 | D. | 12 |
13.已知三角形两边长分别是a,b(b>a),则三角形的周长C应满足( )
| A. | 2b<C<2(a+b) | B. | a+b<C<3b | C. | 2a+b<C<a+2b | D. | 2(a+b)<C<a+3b |
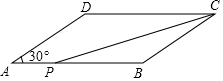 如图,在?ABCD中,AB=8cm,BC=6cm,∠A=30°,点P从点A出发沿线段AB以1m/s的速度向B点移动.
如图,在?ABCD中,AB=8cm,BC=6cm,∠A=30°,点P从点A出发沿线段AB以1m/s的速度向B点移动. 如图,D是△ABC的BA边延长线上的一点,AE是∠DAC的平分线,∠B=∠C,试说明:AE∥BC.
如图,D是△ABC的BA边延长线上的一点,AE是∠DAC的平分线,∠B=∠C,试说明:AE∥BC.