题目内容
11.某公司招聘一名公关人员,对甲、乙、丙、丁四位候选人进行了面试和笔试,他们的成绩如下表所示:| 候选人 | 甲 | 乙 | 丙 | 丁 | |
| 测试成绩 (百分制) | 面试 | 86 | 92 | 90 | 83 |
| 笔试 | 90 | 83 | 83 | 92 | |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
分析 根据题意先算出甲、乙、丙、丁四位候选人的加权平均数,再进行比较,即可得出答案
解答 解:甲的平均成绩为:(86×6+90×4)÷10=87.6(分),
乙的平均成绩为:(92×6+83×4)÷10=88.4(分),
丙的平均成绩为:(90×6+83×4)÷10=87.2(分),
丁的平均成绩为:(83×6+92×4)÷10=86.6(分),
因为乙的平均分数最高,
所以乙将被录取.
故选:B.
点评 此题考查了加权平均数的计算公式,解题的关键是:计算平均数时按6和4的权进行计算.

练习册系列答案
相关题目
3. 如图,已知AB∥CD,BE平分∠ABC,且交CD于点D,∠CDE=150°,则∠C为( )
如图,已知AB∥CD,BE平分∠ABC,且交CD于点D,∠CDE=150°,则∠C为( )
 如图,已知AB∥CD,BE平分∠ABC,且交CD于点D,∠CDE=150°,则∠C为( )
如图,已知AB∥CD,BE平分∠ABC,且交CD于点D,∠CDE=150°,则∠C为( )| A. | 120° | B. | 150° | C. | 135° | D. | 110° |
20.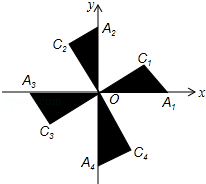 如图,在平面直角坐标系xOy中,Rt△OA1C1,Rt△OA2C2,Rt△OA3C3,Rt△OA4C4…的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4=…=30°.若点A1的坐标为(3,0),OA1=OC2,OA2=OC3,OA3=OC4…,则依此规律,点A2015的纵坐标为( )
如图,在平面直角坐标系xOy中,Rt△OA1C1,Rt△OA2C2,Rt△OA3C3,Rt△OA4C4…的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4=…=30°.若点A1的坐标为(3,0),OA1=OC2,OA2=OC3,OA3=OC4…,则依此规律,点A2015的纵坐标为( )
 如图,在平面直角坐标系xOy中,Rt△OA1C1,Rt△OA2C2,Rt△OA3C3,Rt△OA4C4…的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4=…=30°.若点A1的坐标为(3,0),OA1=OC2,OA2=OC3,OA3=OC4…,则依此规律,点A2015的纵坐标为( )
如图,在平面直角坐标系xOy中,Rt△OA1C1,Rt△OA2C2,Rt△OA3C3,Rt△OA4C4…的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4=…=30°.若点A1的坐标为(3,0),OA1=OC2,OA2=OC3,OA3=OC4…,则依此规律,点A2015的纵坐标为( )| A. | 0 | B. | -3×($\frac{3\sqrt{3}}{2}$)2013 | C. | (2$\sqrt{3}$)2014 | D. | 3×($\frac{2\sqrt{3}}{3}$)2013 |
19.点P是直线l外一点,点A、B、C是直线l上三点,且PA=10,PB=8,PC=6,那么点P到直线l的距离为( )
| A. | 6 | B. | 8 | C. | 不大于6的数 | D. | 小于6的数 |
19.某商品原价168元,经过连续两次降价后的售价为128元,设平均每次降价的百分数为x,则下面所列方程中正确的是( )
| A. | 168(1+x)2=128 | B. | 168(1-x)2=128 | C. | 168(1-2x)2=128 | D. | 168(1-x2)=128 |
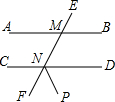 如图,直线AB∥CD,直线EF分别交直线AB、CD于点M、N,NP平分∠DNF,已知∠DNP=55°,则∠EMB=70°.
如图,直线AB∥CD,直线EF分别交直线AB、CD于点M、N,NP平分∠DNF,已知∠DNP=55°,则∠EMB=70°.