题目内容
20.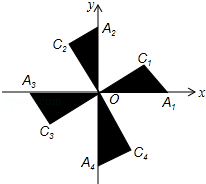 如图,在平面直角坐标系xOy中,Rt△OA1C1,Rt△OA2C2,Rt△OA3C3,Rt△OA4C4…的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4=…=30°.若点A1的坐标为(3,0),OA1=OC2,OA2=OC3,OA3=OC4…,则依此规律,点A2015的纵坐标为( )
如图,在平面直角坐标系xOy中,Rt△OA1C1,Rt△OA2C2,Rt△OA3C3,Rt△OA4C4…的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4=…=30°.若点A1的坐标为(3,0),OA1=OC2,OA2=OC3,OA3=OC4…,则依此规律,点A2015的纵坐标为( )| A. | 0 | B. | -3×($\frac{3\sqrt{3}}{2}$)2013 | C. | (2$\sqrt{3}$)2014 | D. | 3×($\frac{2\sqrt{3}}{3}$)2013 |
分析 根据题意确定出A1,A2,A3,A4…纵坐标,归纳总结得到点A2015的纵坐标与A3纵坐标相同,即可得到结果.
解答 解:∵点A1的坐标为(3,0),OA1=OC2=3,
在Rt△OA2C2中,∠A2OC2=30°,
设A2C2=x,则有OA2=2x,根据勾股定理得:x2+9=4x2,
解得:x=$\sqrt{3}$,即OA2=2$\sqrt{3}$,
∴A2纵坐标为2$\sqrt{3}$,
由OA2=OC3=2$\sqrt{3}$,
在Rt△OA3C3中,∠A3OC3=30°,
设A3C3=y,则有OA3=2y,根据勾股定理得:y2+12=4y2,
解得:y=2,即OA3=4,
∴A3纵坐标为0,
∵2015÷4=503…3,
∴点A2015的纵坐标与A3纵坐标相同,为0.
故选A.
点评 此题考查了规律型:点的坐标,判断出点A2015的纵坐标与A3纵坐标相同是解本题的关键.

练习册系列答案
相关题目
10.已知直线y=x-3与函数y=$\frac{2}{x}$的图象相交于点(a,b),则a2+b2的值是( )
| A. | 13 | B. | 11 | C. | 7 | D. | 5 |
5.我们定义一种变换§:对于一个由5个数组成的数列S1,将其中的每个数换成该数在S1中出现的次数,可得到一个新数列S2.例如:当数列S1是 (4,2,3,4,2)时,经过变换§可得到的新数列S2是(2,2,1,2,2).若数列S1可以由任意5个数组成,则下列的数列可作为S2的是( )
| A. | (1,2,1,2,2) | B. | (2,2,2,3,3) | C. | (1,1,2,2,3) | D. | (1,2,1,1,2) |
11.某公司招聘一名公关人员,对甲、乙、丙、丁四位候选人进行了面试和笔试,他们的成绩如下表所示:
如果公司认为,作为公关人员面试的成绩应该比笔试的成绩更重要,并分别赋予它们6和4的权.公司将录取( )
| 候选人 | 甲 | 乙 | 丙 | 丁 | |
| 测试成绩 (百分制) | 面试 | 86 | 92 | 90 | 83 |
| 笔试 | 90 | 83 | 83 | 92 | |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
7.在-5,0,-2,1这四个数中,最小的数是( )
| A. | -5 | B. | -2 | C. | 0 | D. | 1 |
 已知:如图,∠1=∠2,∠E=∠F,则AB∥CD吗?说明理由.
已知:如图,∠1=∠2,∠E=∠F,则AB∥CD吗?说明理由.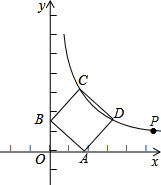 如图,点P($\sqrt{3}$+1,$\sqrt{3}$-1)在双曲线y=$\frac{k}{x}$(x>0)上.
如图,点P($\sqrt{3}$+1,$\sqrt{3}$-1)在双曲线y=$\frac{k}{x}$(x>0)上.