题目内容
6.(1)某厂房屋顶呈人字架形(等腰三角形),如图1所示,已知AC=BC=8m,∠ACB=120°,CD⊥AB于点D.求AB的长度.(2)如图2所示,在平行四边形ABCD中,BE、CF平分∠B、∠C,交AD于E、F两点,求证:AF=DE.
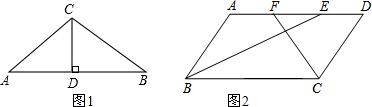
分析 (1)首先计算出∠A=30°,再根据直角三角形的性质可得CD=$\frac{1}{2}$AC=4m,再利用勾股定理计算出AD长,进而可得AB长;
(2)首先根据平行四边形的性质可得AD∥BC,AB=DC,然后证明AB=AE,DC=DF,进而可得AE=FD,再同时减去EF可得AF=DE.
解答 (1)解:∵AC=BC,∠ACB=120°,
∴∠A=∠B=30°.
∵AC=BC,CD⊥AB,
∴AB=2AD.
在Rt△ADC中,∵∠A=30°,AC=8m,
∴CD=4m,
∴$AD=4\sqrt{3}$m,
∴AB=2AD=$8\sqrt{3}$m;
(2)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB=DC.
∴∠AEB=∠EBC.
∵BE平分∠ABC,
∴∠ABE=∠EBC.
∴∠AEB=∠ABE.
∴AB=AE.
同理DC=DF.
∴AE=DF.
∴AE-FE=DF-FE,
即AF=ED.
点评 此题主要考查了勾股定理的应用、直角三角形的性质、平行四边形的性质,关键是掌握平行四边形对边平行且相等.

练习册系列答案
相关题目
11.某公司招聘一名公关人员,对甲、乙、丙、丁四位候选人进行了面试和笔试,他们的成绩如下表所示:
如果公司认为,作为公关人员面试的成绩应该比笔试的成绩更重要,并分别赋予它们6和4的权.公司将录取( )
| 候选人 | 甲 | 乙 | 丙 | 丁 | |
| 测试成绩 (百分制) | 面试 | 86 | 92 | 90 | 83 |
| 笔试 | 90 | 83 | 83 | 92 | |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
14.若a>b,则下列不等式成立的是( )
| A. | a-1<b-1 | B. | -3a>-2b | C. | a>b-16 | D. | $\frac{a}{5}<\frac{b}{5}$ |
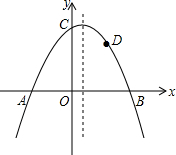 如图,抛物线y=-$\frac{1}{2}$x2+bx+c与x轴交于A、B两点,与y轴交于点C,且OA=2,OC=3.
如图,抛物线y=-$\frac{1}{2}$x2+bx+c与x轴交于A、B两点,与y轴交于点C,且OA=2,OC=3.